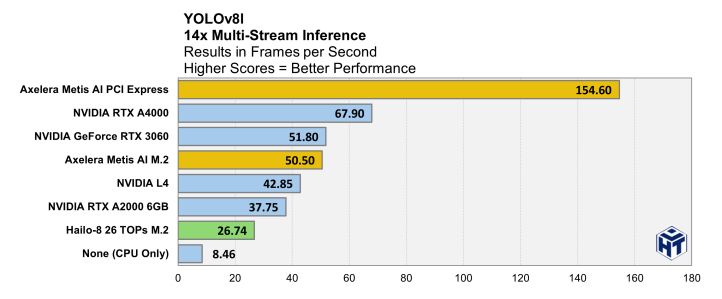
- 230% faster
- 330% more power efficient
and also about 3x cheaper
- 230% faster
- 330% more power efficient
and also about 3x cheaper

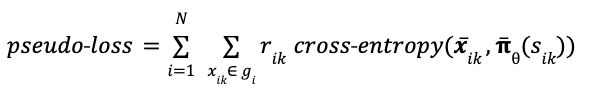
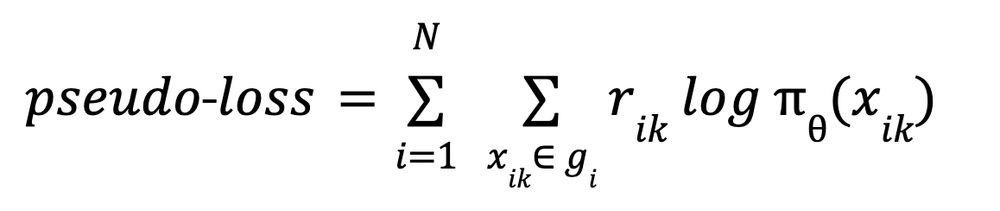

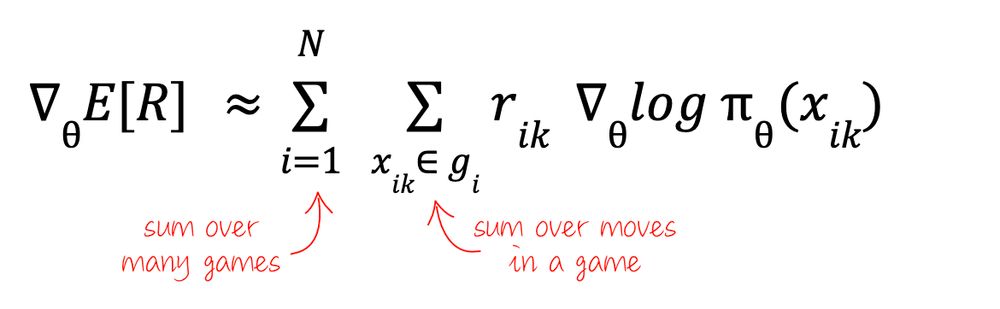
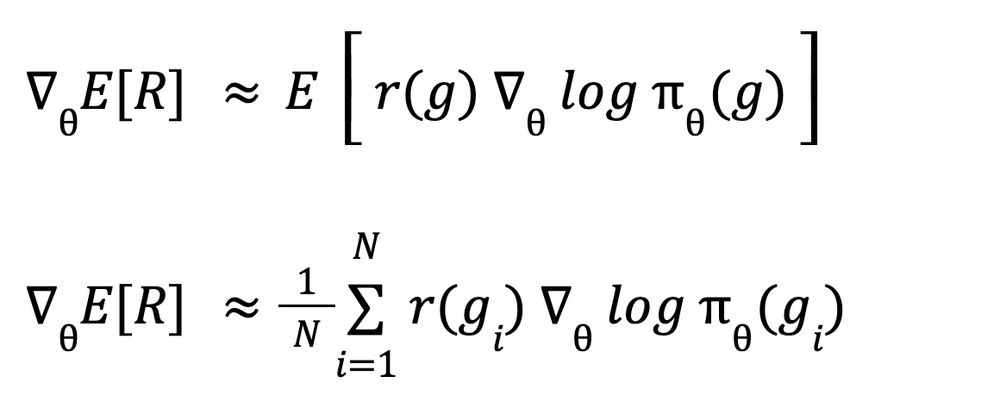
First, we use our policy network 𝛑 to approximate the move probabilities.
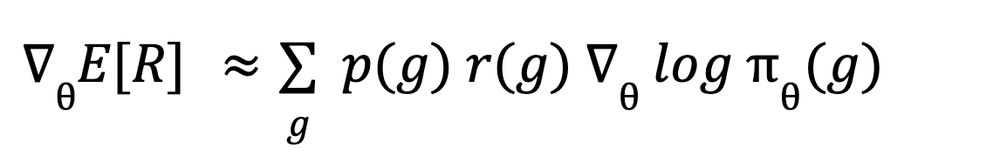
First, we use our policy network 𝛑 to approximate the move probabilities.
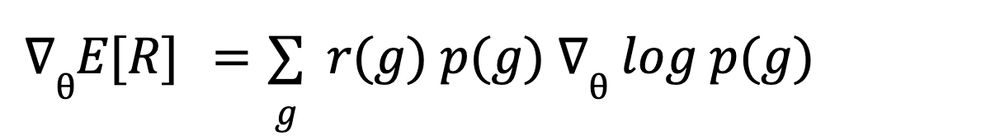

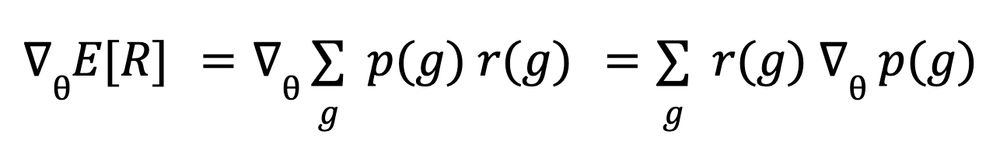
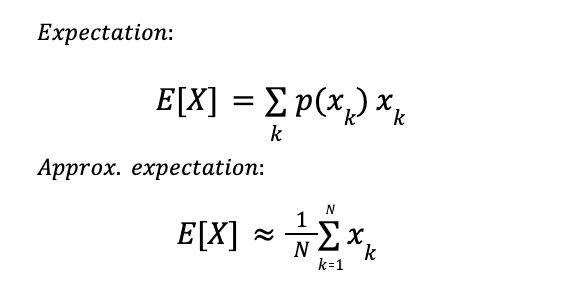
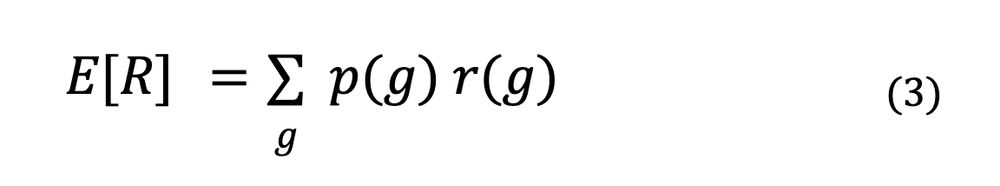



Let's set the stage: wether playing pong (single-player against a deterministic algorithm) or predicting the next token or sentence in a chain-of-thought LLM, the idea is the same:
Let's set the stage: wether playing pong (single-player against a deterministic algorithm) or predicting the next token or sentence in a chain-of-thought LLM, the idea is the same:
I'd like to revisit the basic math of RL to see why. Let's enter the dungeon!

I'd like to revisit the basic math of RL to see why. Let's enter the dungeon!
Colab here, checking this on Gemma2 9B: colab.research.google.com/drive/1Igzf...
Bottom line: 99% of them are in the 0.1 - 1.1 range. I'm not sure partitioning them into "large" and "small" makes that much sense...

Colab here, checking this on Gemma2 9B: colab.research.google.com/drive/1Igzf...
Bottom line: 99% of them are in the 0.1 - 1.1 range. I'm not sure partitioning them into "large" and "small" makes that much sense...
- that the fine-tuning data distribution if close to the pre-training one
Both questionable IMHO, so I won't detail the math.
Some results:

- that the fine-tuning data distribution if close to the pre-training one
Both questionable IMHO, so I won't detail the math.
Some results:





In this representation, it's easy to see that you can split the sum in two. And this is what the split looks like on matrices:

In this representation, it's easy to see that you can split the sum in two. And this is what the split looks like on matrices:

