We go back to 1️⃣ and use the content-context connection to show that the higher is the mutual information between data and its positional representation, the better is task performance.
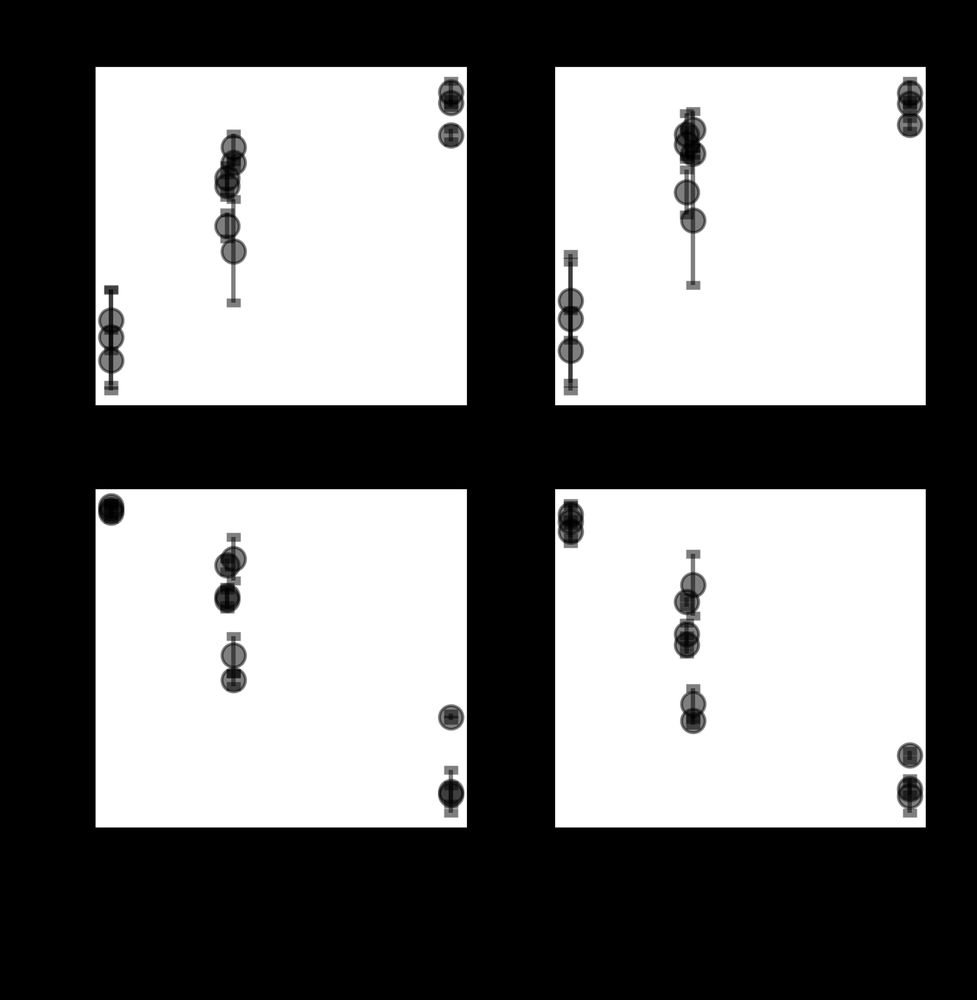
We go back to 1️⃣ and use the content-context connection to show that the higher is the mutual information between data and its positional representation, the better is task performance.
How does RoPEPool compare to RoPE and F-StrIPE? Our analysis with a toy example says: RoPEPool isn’t just different, it’s also richer in terms of expressivity.
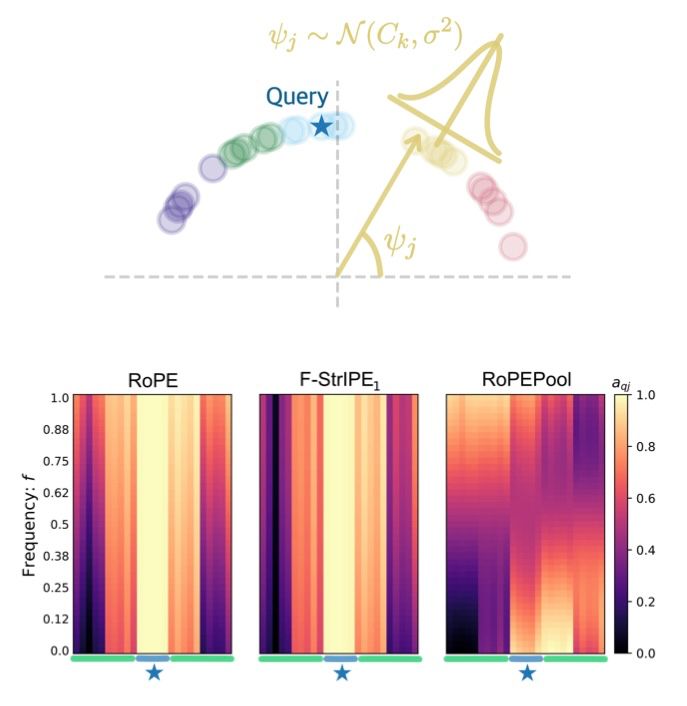
How does RoPEPool compare to RoPE and F-StrIPE? Our analysis with a toy example says: RoPEPool isn’t just different, it’s also richer in terms of expressivity.
It’s not just vibes - we characterize precisely how queries and keys are affected by positional information.

It’s not just vibes - we characterize precisely how queries and keys are affected by positional information.
Curious? Check out the companion webpage: bit.ly/faststructurepe
Curious? Check out the companion webpage: bit.ly/faststructurepe
Enter Stochastic Positional Encoding! It brings relative positional information back into the picture without going to quadratic cost.
Enter Stochastic Positional Encoding! It brings relative positional information back into the picture without going to quadratic cost.
This was the idea used by Performers, for example.
This was the idea used by Performers, for example.
This makes it really hard to apply them to lengthy sequences, like music, where long-term connections carry important information.
This makes it really hard to apply them to lengthy sequences, like music, where long-term connections carry important information.


