Daniel Litt
@littmath.bsky.social
Assistant professor (of mathematics) at the University of Toronto. Algebraic geometry, number theory, forever distracted and confused, etc. He/him.
back on the good stuff (geodesic dome tourism)
August 23, 2025 at 11:28 PM
back on the good stuff (geodesic dome tourism)
planning to use this picture in a talk to explain what a foliation is, feeling extremely Canadian
July 24, 2025 at 3:46 PM
planning to use this picture in a talk to explain what a foliation is, feeling extremely Canadian
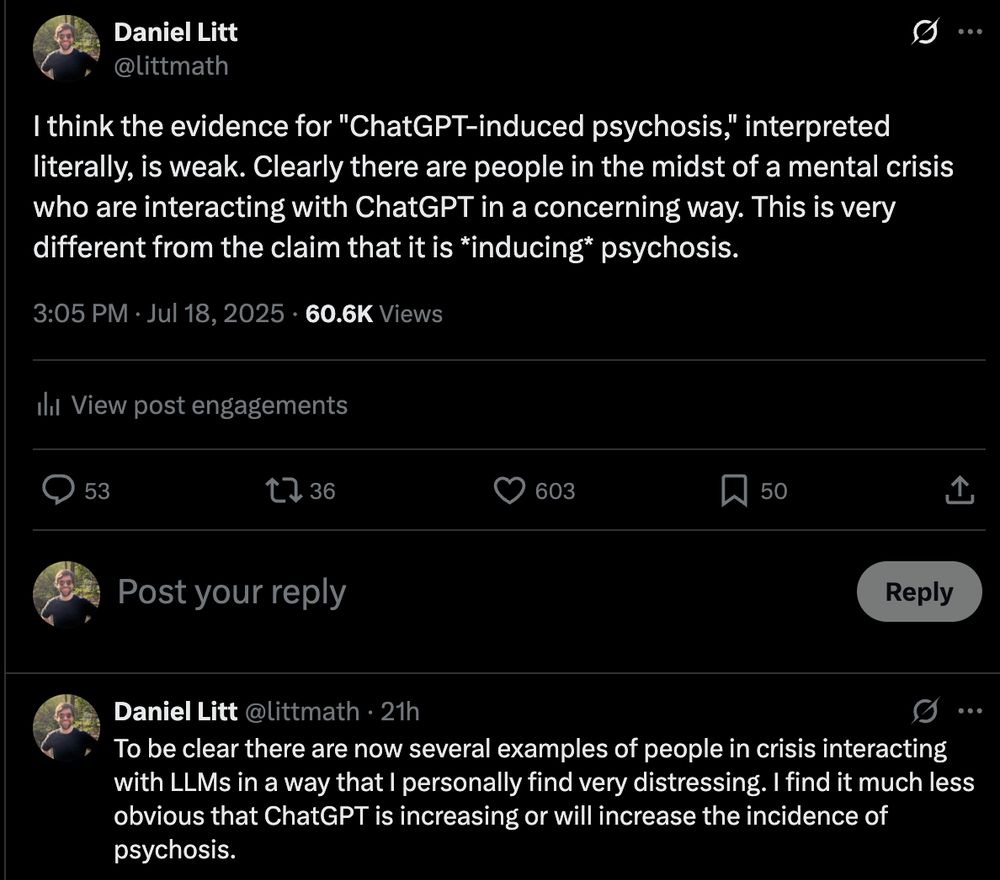
Getting a lot of heat for this on the other site.
July 19, 2025 at 4:57 PM
Getting a lot of heat for this on the other site.
it was a perfect summer day in Toronto. the sun was out; the subway station garbage bags danced upside-down in the wind
July 18, 2025 at 4:59 PM
it was a perfect summer day in Toronto. the sun was out; the subway station garbage bags danced upside-down in the wind
on the other hand, guitars are predominantly anti-fascist machines
July 9, 2025 at 3:26 PM
on the other hand, guitars are predominantly anti-fascist machines
“we have an ellipsoid at home” / the ellipsoid at home
July 7, 2025 at 9:27 PM
“we have an ellipsoid at home” / the ellipsoid at home
July 2, 2025 at 2:47 PM
New paper with my postdoc Simone Coccia!
July 2, 2025 at 2:47 PM
New paper with my postdoc Simone Coccia!
yes I’m worried about x-risk, why do you ask?
June 23, 2025 at 11:02 PM
yes I’m worried about x-risk, why do you ask?
I asked a MathOverflow question. Please tell me if you know the answer! mathoverflow.net/questions/49...
June 23, 2025 at 7:43 PM
I asked a MathOverflow question. Please tell me if you know the answer! mathoverflow.net/questions/49...
9% chance of catgirl dystopia
June 22, 2025 at 6:32 PM
9% chance of catgirl dystopia
dyson sphere betting odds
June 21, 2025 at 6:27 PM
dyson sphere betting odds
Incredibly bad (changes to N.S.F. funding for math):
May 22, 2025 at 7:50 PM
Incredibly bad (changes to N.S.F. funding for math):
![Robert Francis Prevost was born in Chicago on 14 September 1955, the son of Louis Marius Prevost and Mildred Martínez.[4] His father, who was a United States Navy veteran of World War II and school administrator,[5] was of French and Italian descent, and his mother of Spanish descent.[6] As a child, Prevost served as an altar boy at St. Mary of the Assumption Church on the far South Side of Chicago.[7] He completed his secondary studies at the minor seminary of the Order of St. Augustine in 1973. Prevost earned a Bachelor of Science degree in mathematics at Villanova University in 1977.[8]](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:wvexgwndckqyszwviyuoeibi/bafkreiab6e3zx37wlvxtahxnpfjpgngci34k3l2o27vr2bhiniiglkydtm@jpeg)
parent of toddler moment
February 11, 2025 at 12:51 AM
parent of toddler moment
For example, we are able to check it for many solutions to the Schlesinger Painlevé VI equations (below). 19/n
January 24, 2025 at 5:12 PM
For example, we are able to check it for many solutions to the Schlesinger Painlevé VI equations (below). 19/n
The main point of the paper is that we can actually prove this conjecture in lots of cases, both for linear, and non-linear differential equations. For example, it's true for the differential equation satisfied by the function F(t) below (which we saw earlier). 16/n
January 24, 2025 at 5:12 PM
The main point of the paper is that we can actually prove this conjecture in lots of cases, both for linear, and non-linear differential equations. For example, it's true for the differential equation satisfied by the function F(t) below (which we saw earlier). 16/n
Just a quick note--it's really important that one takes the Taylor expansion at a point where the differential equation is non-singular. Otherwise there are lots of counterexamples, for example, the one below. 14/n
January 24, 2025 at 5:12 PM
Just a quick note--it's really important that one takes the Taylor expansion at a point where the differential equation is non-singular. Otherwise there are lots of counterexamples, for example, the one below. 14/n
Eisenstein showed that the Taylor expansions of algebraic functions have a special property: only finitely many primes appear in the denominators of their coefficients. We conjecture that this property characterizes algebraic solutions to algebraic differential equations. 12/n
January 24, 2025 at 5:12 PM
Eisenstein showed that the Taylor expansions of algebraic functions have a special property: only finitely many primes appear in the denominators of their coefficients. We conjecture that this property characterizes algebraic solutions to algebraic differential equations. 12/n
Here's the conjecture. It's not hard to see that a differential equation like the one below (with g a rational function, say) always has local solutions where g is defined--you can just write out their Taylor expansions and check convergence. 11/n
January 24, 2025 at 5:12 PM
Here's the conjecture. It's not hard to see that a differential equation like the one below (with g a rational function, say) always has local solutions where g is defined--you can just write out their Taylor expansions and check convergence. 11/n
The standard way to formalize it, due I think to Lazarus Fuchs in 1875, is to ask when a differential equation has an *algebraic* solution, i.e. one that also satisfies a polynomial. That is, a function is algebraic if it can be defined implicitly by polynomials. 6/n
January 24, 2025 at 5:12 PM
The standard way to formalize it, due I think to Lazarus Fuchs in 1875, is to ask when a differential equation has an *algebraic* solution, i.e. one that also satisfies a polynomial. That is, a function is algebraic if it can be defined implicitly by polynomials. 6/n
The basic question this paper is about is: when can you write down the solution to a differential equation (say, of the form below) explicitly. In fact this has been one of the animating questions of mathematics since the mid-1800s. 5/n
January 24, 2025 at 5:12 PM
The basic question this paper is about is: when can you write down the solution to a differential equation (say, of the form below) explicitly. In fact this has been one of the animating questions of mathematics since the mid-1800s. 5/n
For example, when can you solve a polynomial by radicals? Can you construct a regular n-gon using only a compass and straightedge? 4/n
January 24, 2025 at 5:12 PM
For example, when can you solve a polynomial by radicals? Can you construct a regular n-gon using only a compass and straightedge? 4/n