So you can see why, in being so opposite of the people now in power, they become the enemy.
So you can see why, in being so opposite of the people now in power, they become the enemy.
Clément Bonet, Kimia Nadjahi, Thibault Sejourne, Kilian FATRAS, Nicolas Courty
Action editor: Benjamin Guedj
https://openreview.net/forum?id=AjJTg5M0r8
#transport #outliers #optimal
Clément Bonet, Kimia Nadjahi, Thibault Sejourne, Kilian FATRAS, Nicolas Courty
Action editor: Benjamin Guedj
https://openreview.net/forum?id=AjJTg5M0r8
#transport #outliers #optimal

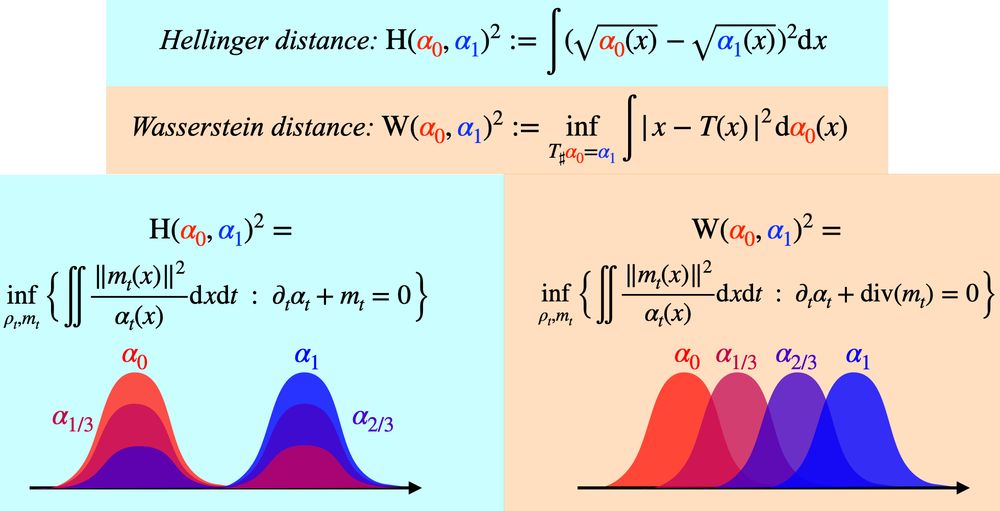
Quote:
“The relevance of the identifications of concepts stated in Eulerian terms with those stated in Lagrangian terms is not sufficiently recognized when everything is smooth.”

Quote:
“The relevance of the identifications of concepts stated in Eulerian terms with those stated in Lagrangian terms is not sufficiently recognized when everything is smooth.”
On 27th / 28th April 2025 in Singapore 🇸🇬, this popular event returns with a fresh organizing team 👇 & bold new ideas 🧠 to explore bridging AI & life sciences 🧬


