Compared to samples from RevBayes, an MCMC method, we can see that PF2 is broadly in agreement albeit with a smoother distribution. Since PF2 is amortized, it can sample from the posterior much faster than MCMC methods.

16/17

Under complex evolution models (e.g. accounting for co-evolution or selection) where the likelihood is not computable, PF2 really shines further improving on the PF1 performance gain over maximum-likelihood methods.

15/17

PF2 has a smaller memory footprint than PF1, despite having more parameters. It can run an order of magnitude faster than even FastME when only sampling topologies.

14/17

We trained 2 PF2 models under LG, a simple model where maximum-likelihood methods shine. PF2 estimates full tree posteriors, while PF2topo only estimates the posterior of the tree topology.
Both models outperform all other methods significantly for smaller trees.

13/17

At inference time, we can sample trees by iteratively sampling merges and branch lengths from the learned conditional merge and branch-length distributions.

12/17

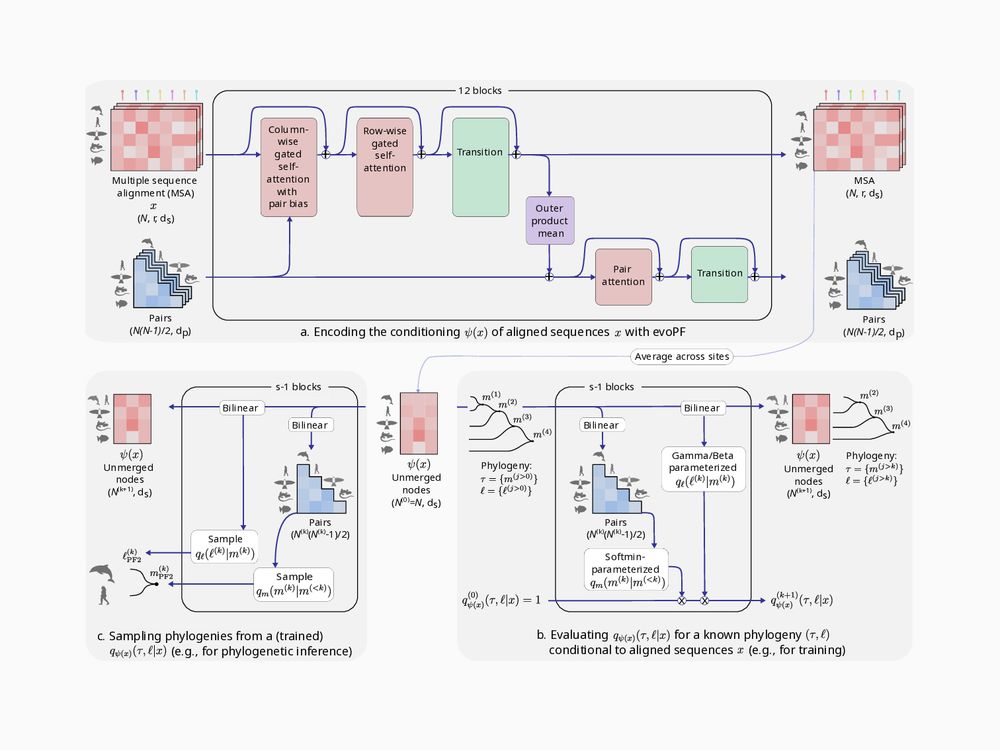
Our probability estimation network, BayesNJ, is also parametrized and learnable. It is jointly optimized with the embedding network EvoPF during training.

11/17

To estimate the posterior, we describe trees as an ordered succession of pairwise merges. Allowing us to factorize the total tree probability as the product of successive conditional merge probabilities.

10/17

Our embedding network, EvoPF, is inspired from EvoFormer and keeps mutually updating representations of sequences and sequence pairs. It is much more scalable than PF1, allowing us to us 250x more learnable parameters than PF1 with a similar memory footprint.

9/17

Once trained, we can embed empirical sequences into the learned latent space and sample trees from the learned posterior, without ever having to compute a likelihood.

8/17

PF2 estimates the posterior probability of a tree by (1) embedding sequences into a latent space, then (2) estimating the posterior from that latent space.
PF2 is optimized by minimizing the estimated log-posterior over many (tree, sequences) pairs sampled under a given probabilistic model.

7/17

Our first attempt, PF1, used pairwise distances as a proxy learning target. This worked reasonably well, but using a proxy yields a gap in topological accuracy w.r.t maximum likelihood methods.
(see doi.org/10.1093/molb...)

5/17

Likelihood-free/simulation-based inference can solve this issue.
It allows for inference under complex models where sampling is easy but likelihood computations costly or impossible.
It's an alternative way to access the model.

4/17

Maximum-likelihood based tree inference searches for the most likely tree over the sequences.
This yields accurate estimates but can be slow and limits us to evolution models for which we can compute the likelihood.

3/17

Phylogenetic trees describe the shared evolutionary history of a set of related genomic sequences (at the leaves) from a common ancestor (at the root).
The topology describes this ancestry, while the branch lengths describe some measure of how related or distant sequences at each end are.

2/17

We’re very excited to finally share our latest work:
Phyloformer 2, a deep end-to-end phylogenetic reconstruction method: arxiv.org/abs/2510.12976
Using neural posterior estimation, it outperforms Phyloformer 1 and maximum-likelihood methods under simple and complex evolutionary models.

🧵1/17