Perinatal Demography • Mortality • Uncertainty • Dataviz










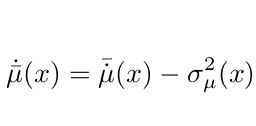

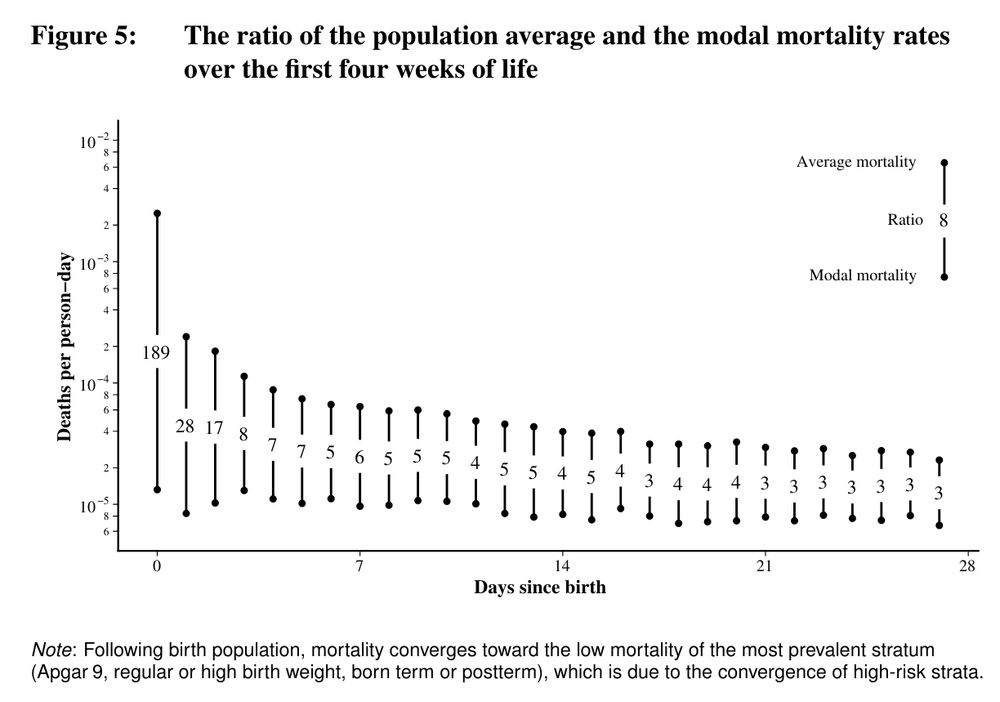
As the average death rate in a cohort of newborns declines over the first month of life, the variance of death rates declines as well in a power-law fashion. Read more in my piece on post-natal mortality selection and convergence.

As the average death rate in a cohort of newborns declines over the first month of life, the variance of death rates declines as well in a power-law fashion. Read more in my piece on post-natal mortality selection and convergence.