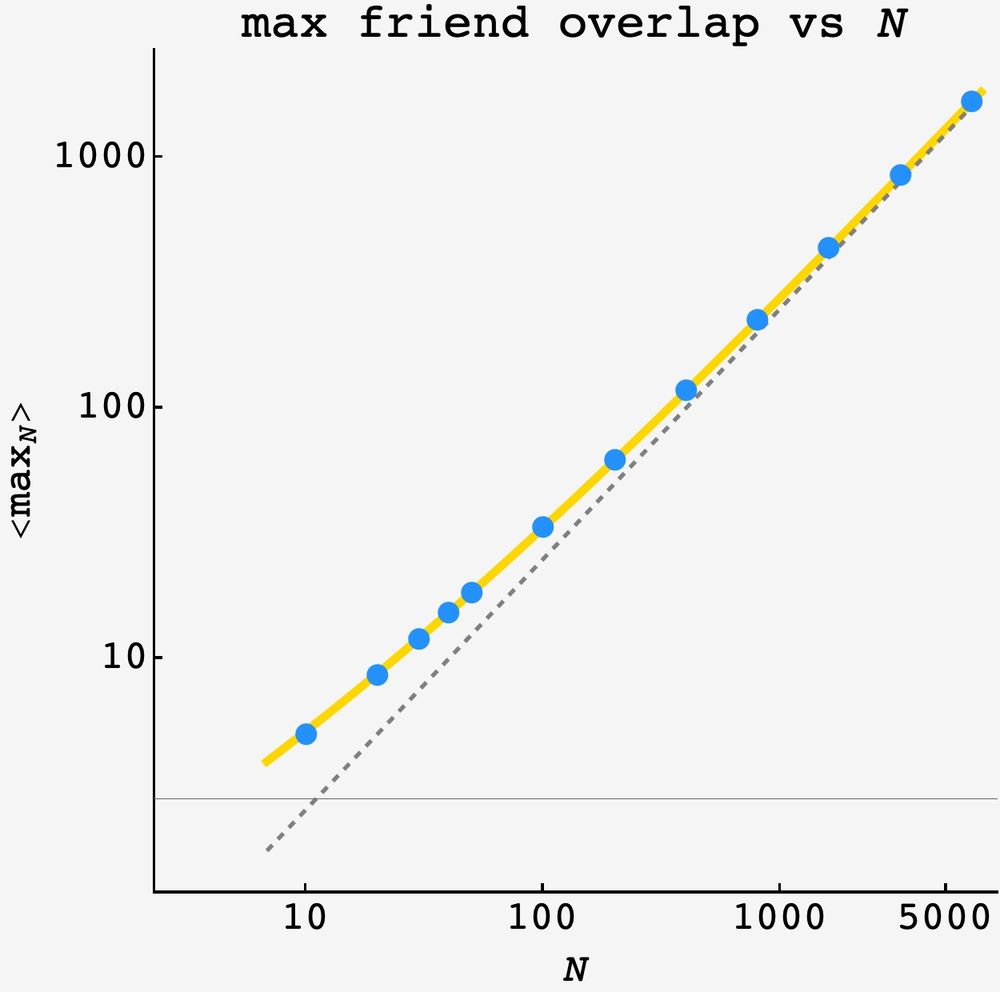
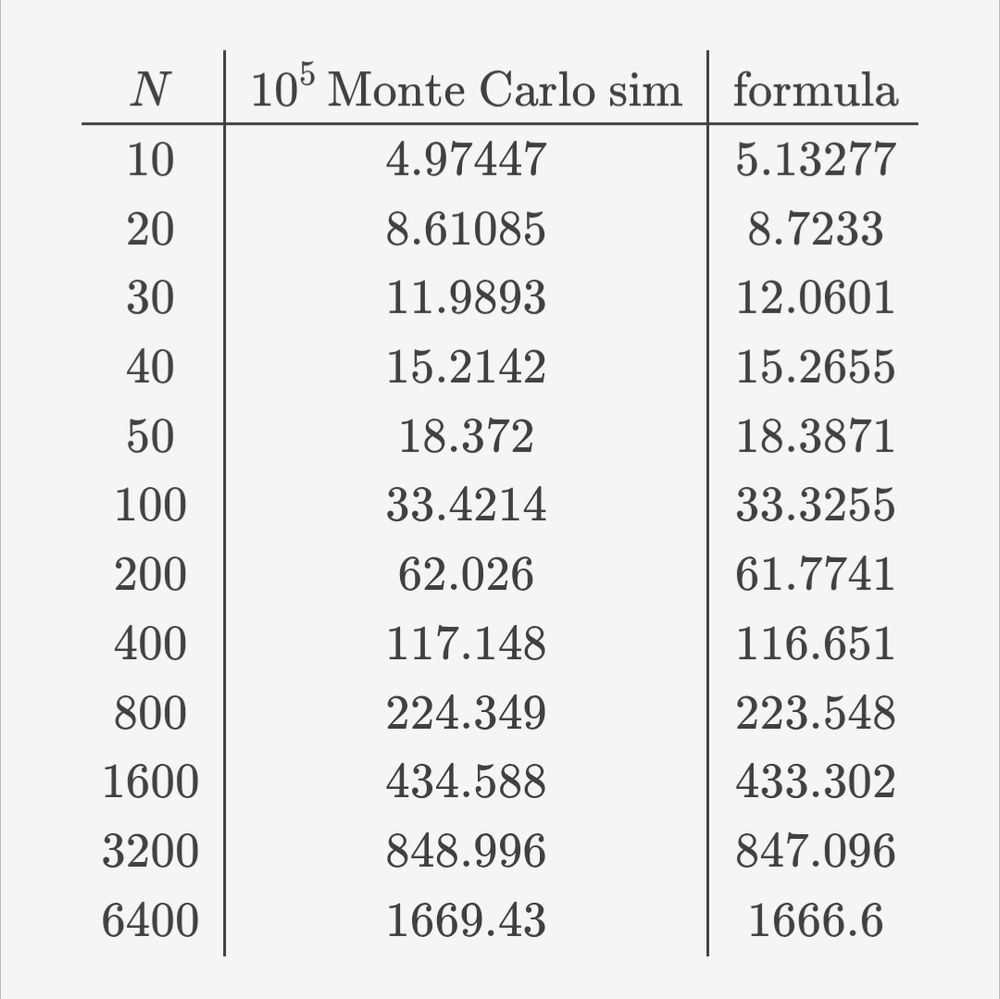
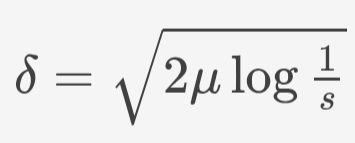
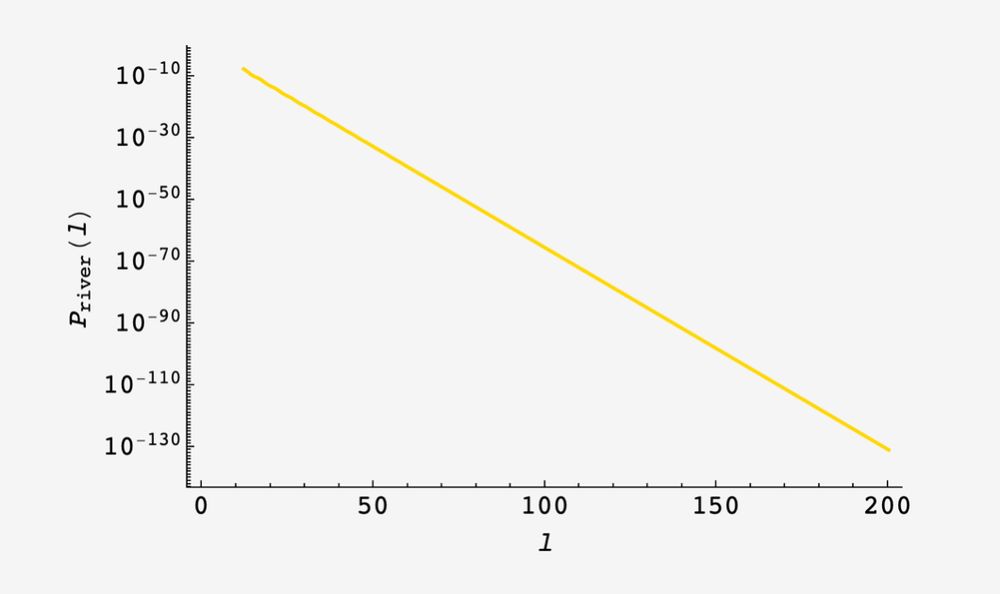
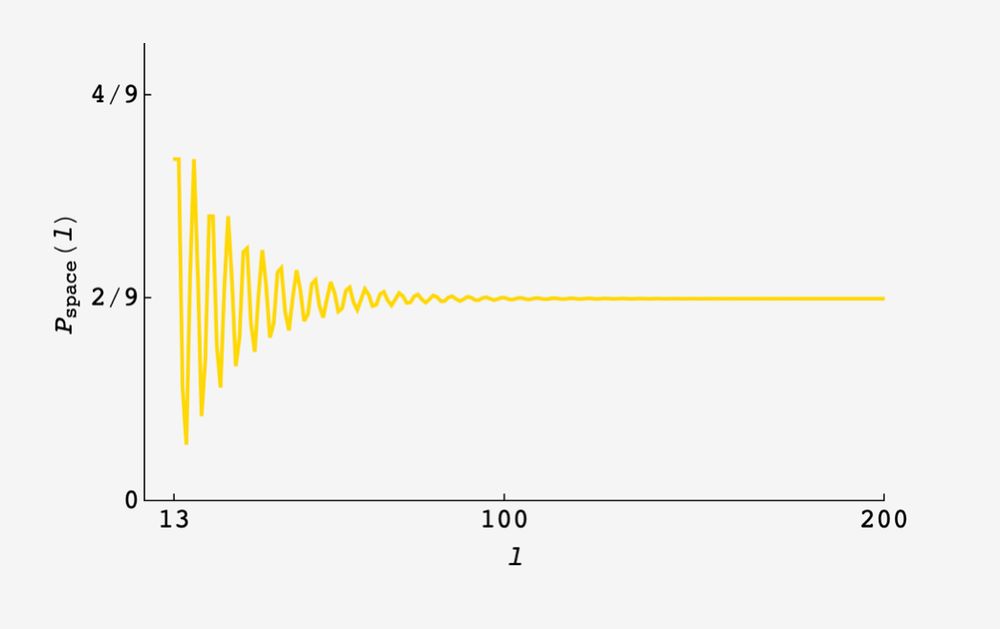
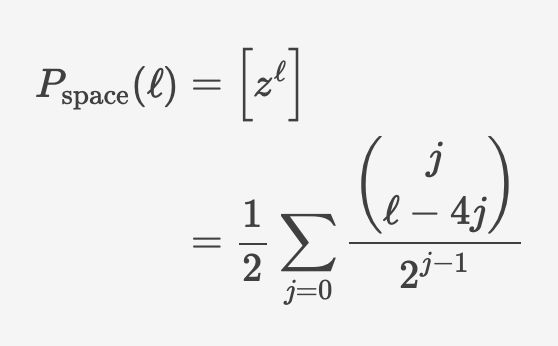
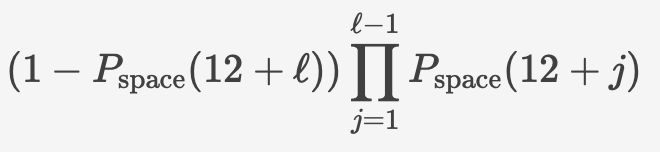
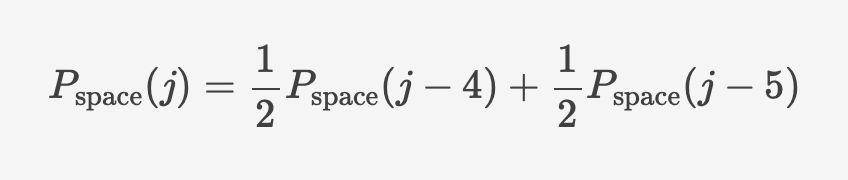
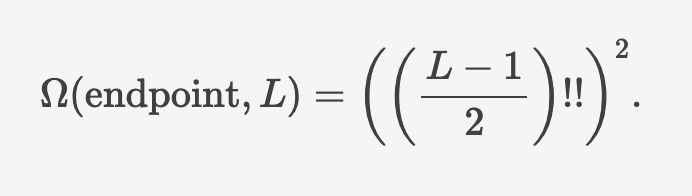
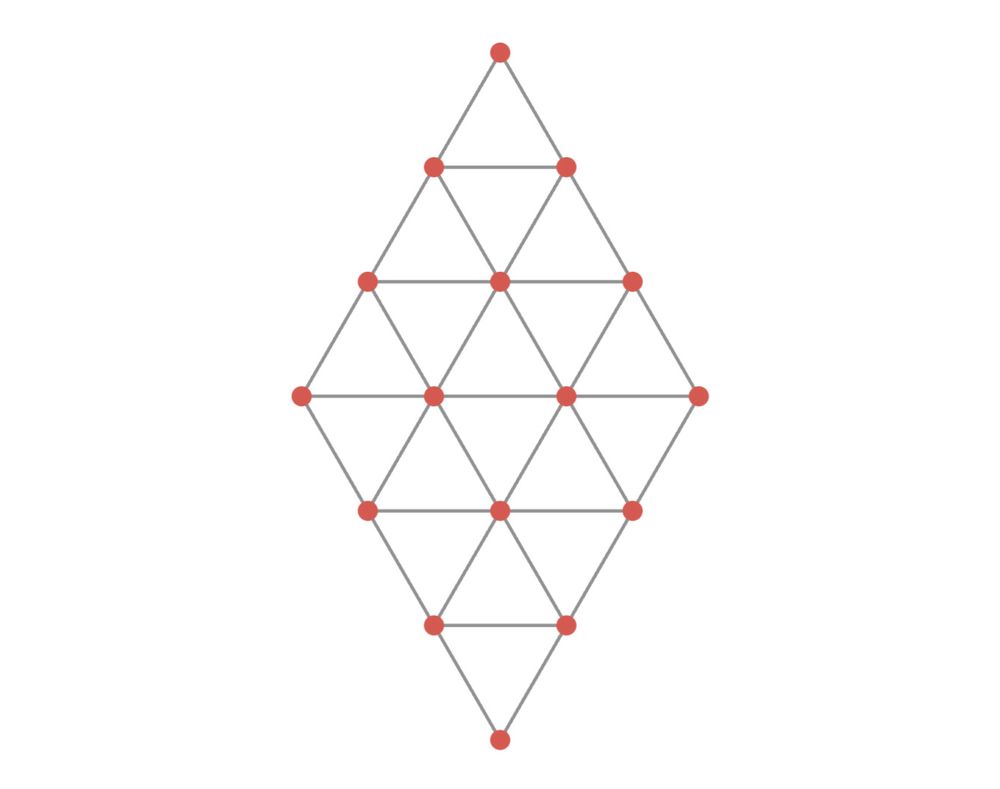
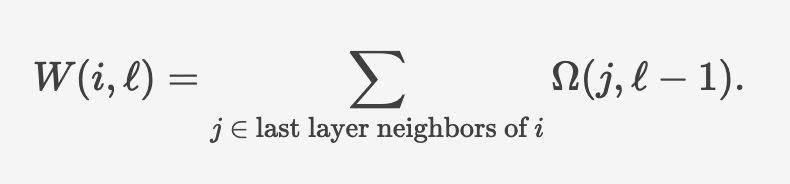
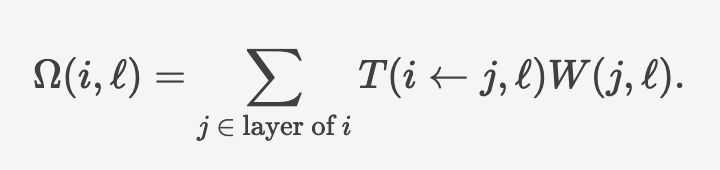
the blue points are the result of a 1E6 round simulation and the gold point are the formula above.
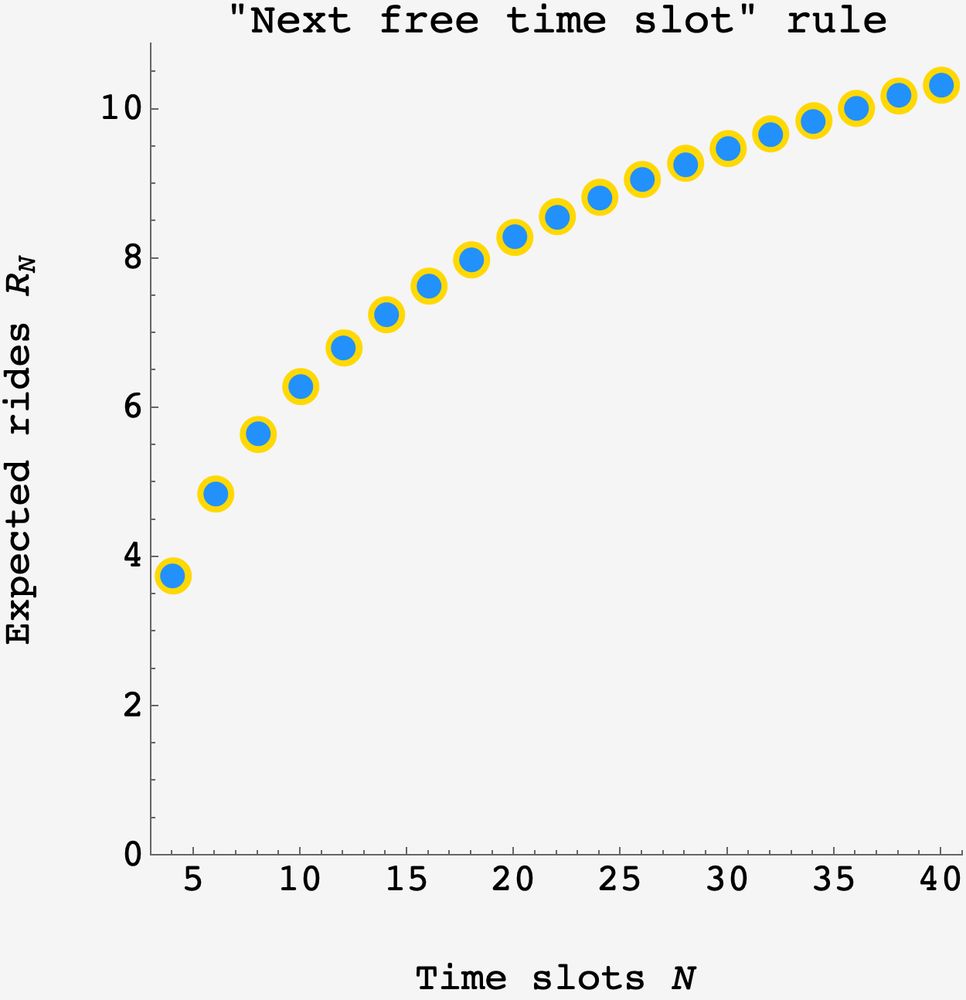
the blue points are the result of a 1E6 round simulation and the gold point are the formula above.
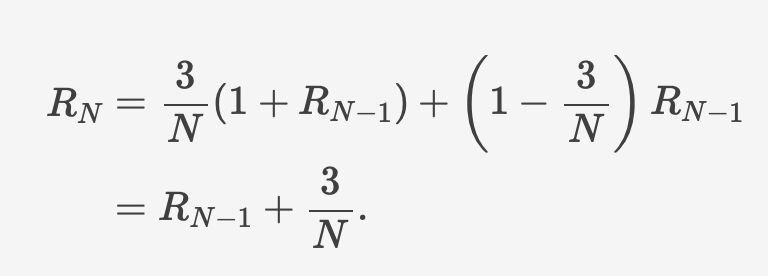

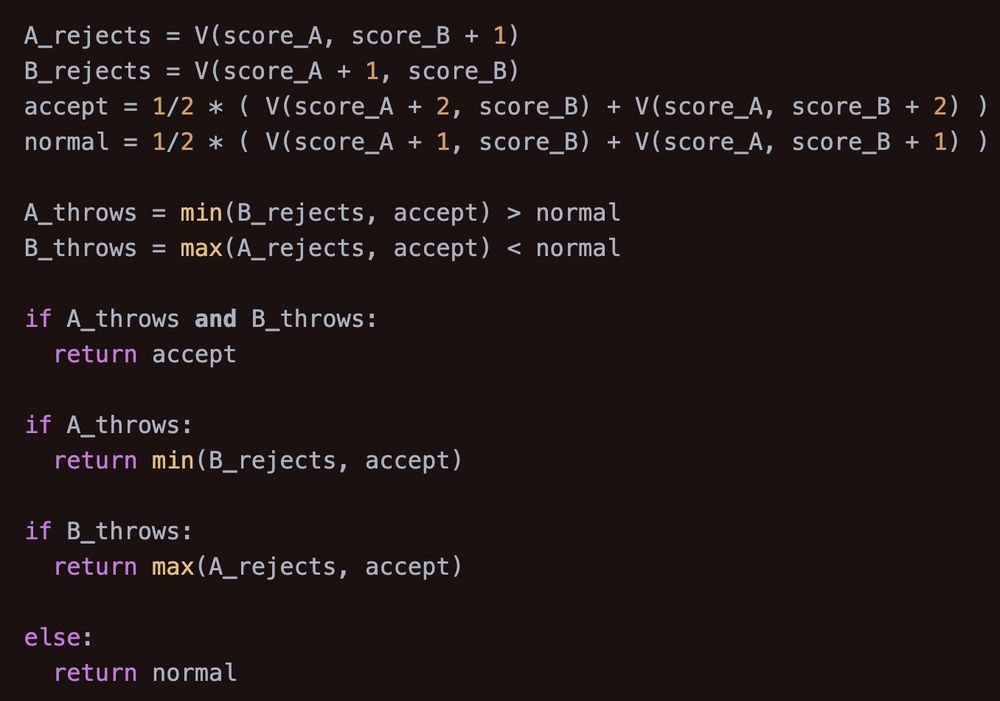




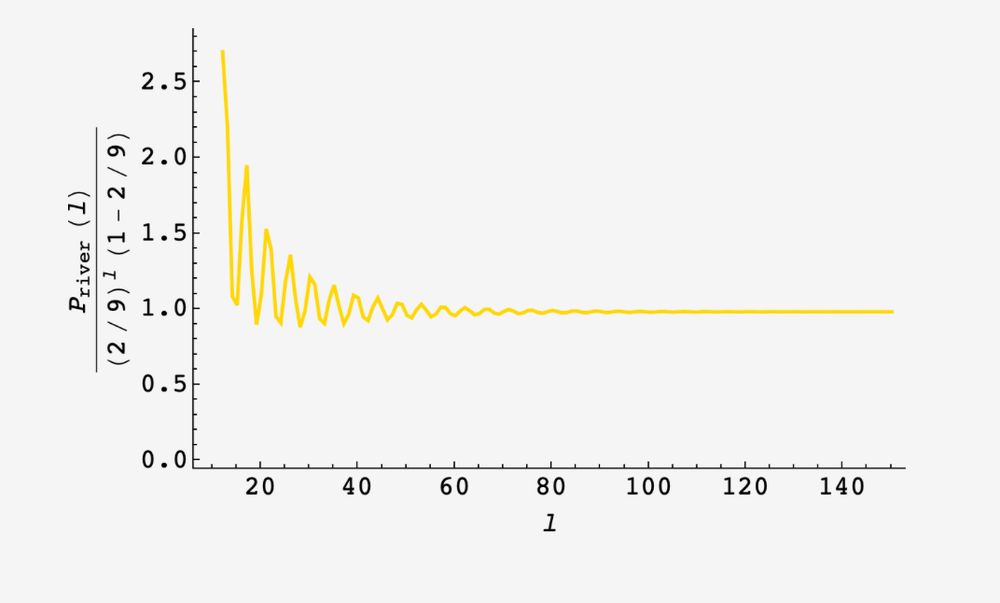
but we can better capture the plight of the everyman beachgoer with the median distance. binary searching the cdf, we find the 50th percentile beach distance is approximately 0.17426
@xaqwg.bsky.social
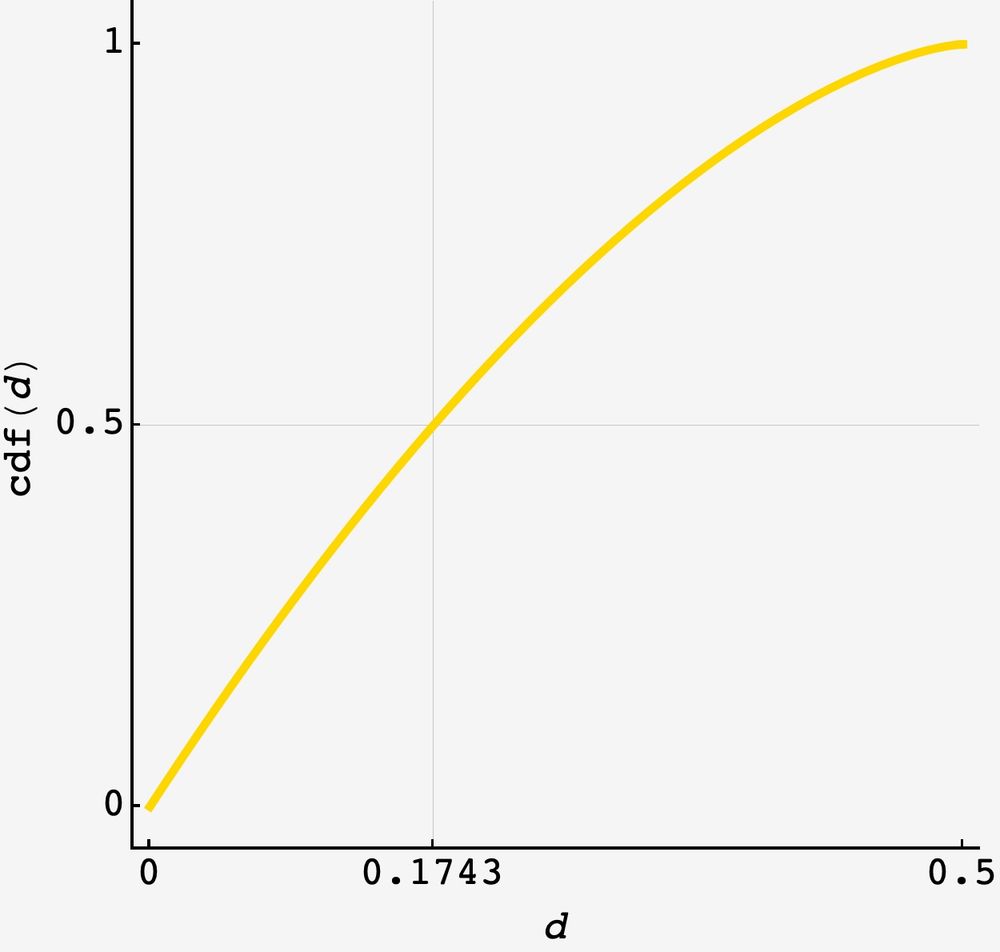
but we can better capture the plight of the everyman beachgoer with the median distance. binary searching the cdf, we find the 50th percentile beach distance is approximately 0.17426
@xaqwg.bsky.social


joshmaxsilverman.github.io/2025-03-16-f...
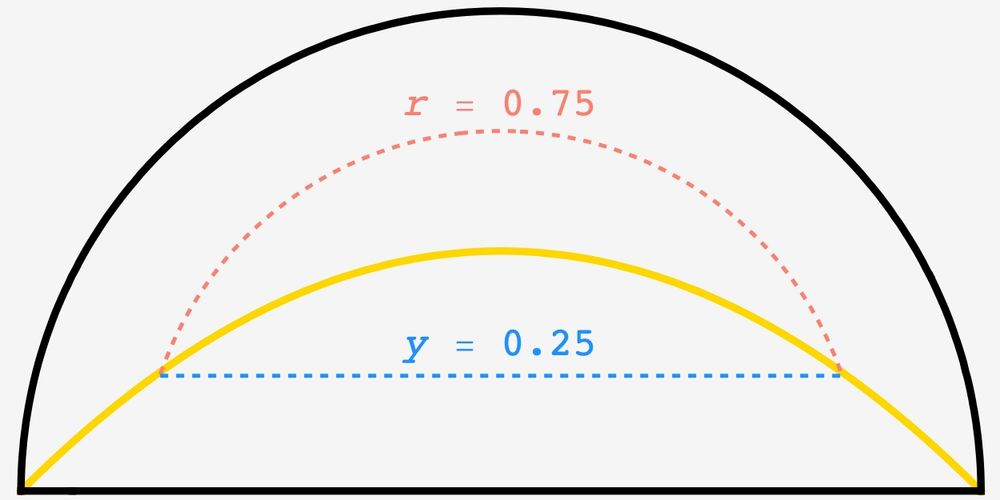
joshmaxsilverman.github.io/2025-03-16-f...

