Joseph O'Rourke
@josephorourke.bsky.social
Mathematician and Computer Scientist, Smith College, USA.
https://cs.smith.edu/~jorourke/
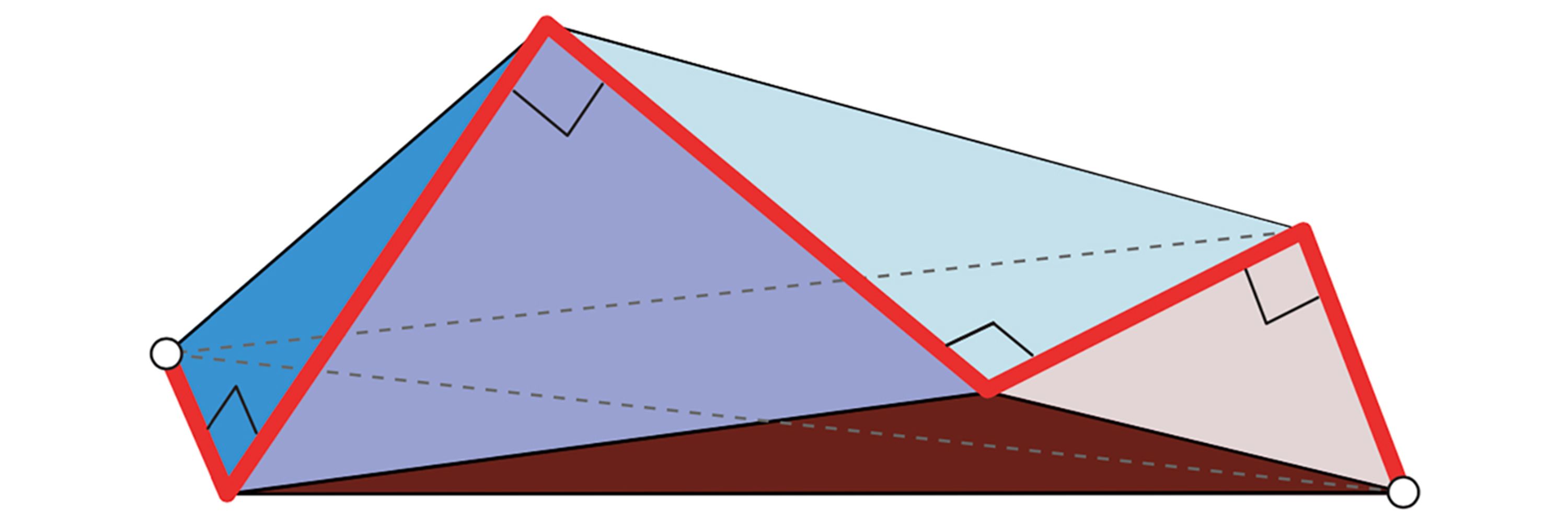
Polyhedron displayed in banner has max volume of all foldings from a square.
https://cs.smith.edu/~jorourke/
Polyhedron displayed in banner has max volume of all foldings from a square.
Cambridge University Press.
www.cambridge.org/core/books/m...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt
www.cambridge.org/core/books/m...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt
November 5, 2025 at 3:04 PM
Cambridge University Press.
www.cambridge.org/core/books/m...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt
www.cambridge.org/core/books/m...
#MathSky #Mathematics 🧪 #Geometry #Origami #MathArt
In fact in this example, 3 guards suffice. Minimal guarding is an NP-hard problem, i.e., intractable.
#Mathematics #MathSky #GraphTheory
www.science.smith.edu/~jorourke/bo...
#Mathematics #MathSky #GraphTheory
www.science.smith.edu/~jorourke/bo...
November 2, 2025 at 11:11 PM
In fact in this example, 3 guards suffice. Minimal guarding is an NP-hard problem, i.e., intractable.
#Mathematics #MathSky #GraphTheory
www.science.smith.edu/~jorourke/bo...
#Mathematics #MathSky #GraphTheory
www.science.smith.edu/~jorourke/bo...
These triangles are known to have a periodic billiard path: (1) All acute triangles. (2) All right triangles. (3) All rational triangles. (4) All obtuse triangles with obtuse angle smaller than 5 pi/8 (the 112.4 deg that I quoted). #MathSky #Mathematics #Geometry #Billiards
October 22, 2025 at 3:50 PM
These triangles are known to have a periodic billiard path: (1) All acute triangles. (2) All right triangles. (3) All rational triangles. (4) All obtuse triangles with obtuse angle smaller than 5 pi/8 (the 112.4 deg that I quoted). #MathSky #Mathematics #Geometry #Billiards
Sharp eyes to notice the two perpendicular bounces. Probably not for all triangles, I agree.
October 18, 2025 at 5:40 PM
Sharp eyes to notice the two perpendicular bounces. Probably not for all triangles, I agree.
Beautiful indeed. And with recent results from the study of translation surfaces.
October 18, 2025 at 2:31 PM
Beautiful indeed. And with recent results from the study of translation surfaces.
Sure. Have them email me, jorourke@smith.edu.
September 27, 2025 at 1:11 PM
Sure. Have them email me, jorourke@smith.edu.
See also: "Why can't a nonabelian group be 75% abelian?" mathoverflow.net/q/211159/6094
September 25, 2025 at 4:48 PM
See also: "Why can't a nonabelian group be 75% abelian?" mathoverflow.net/q/211159/6094
I wonder in which dimensions is the cylinder/sphere volume ratio rational?
#Mathematics #MathSky #Geometry
#Mathematics #MathSky #Geometry
September 14, 2025 at 12:34 AM
I wonder in which dimensions is the cylinder/sphere volume ratio rational?
#Mathematics #MathSky #Geometry
#Mathematics #MathSky #Geometry
p.4 of their paper details the construction. "the Noperthedron has 3·30=90 vertices." They set three pts C1,C2,C3 and then apply the cyclic group C_30 to each.
August 31, 2025 at 2:01 AM
p.4 of their paper details the construction. "the Noperthedron has 3·30=90 vertices." They set three pts C1,C2,C3 and then apply the cyclic group C_30 to each.
The Rupert property requires the convex polyhedron P to tunnel by translation through an isometric copy of P. I wonder if twisting while translating would permit any P---even the "Noperthedron"---to pass through itself? #Mathematics #Geometry #MathSky
August 28, 2025 at 10:02 PM
The Rupert property requires the convex polyhedron P to tunnel by translation through an isometric copy of P. I wonder if twisting while translating would permit any P---even the "Noperthedron"---to pass through itself? #Mathematics #Geometry #MathSky
Yes, the authors clearly had fun! :-)
August 27, 2025 at 9:06 PM
Yes, the authors clearly had fun! :-)
*Visual Complex Analysis* by Tristan Needham. global.oup.com/academic/pro...
global.oup.com
June 25, 2025 at 5:54 PM
*Visual Complex Analysis* by Tristan Needham. global.oup.com/academic/pro...
Henry Cohn figured that out: Again, not the cube:
mathoverflow.net/a/73941/6094
mathoverflow.net/a/73941/6094

Optimal 8-vertex isoperimetric polyhedron?
I know from Marcel Berger's
Geometry Revealed:
A Jacob's Ladder to Modern Higher Geometry
(p.531)
that it is not yet established which polyhedron in $\mathbb{R}^3$ on 8 vertices achieves the optimal
mathoverflow.net
June 10, 2025 at 12:25 PM
Henry Cohn figured that out: Again, not the cube:
mathoverflow.net/a/73941/6094
mathoverflow.net/a/73941/6094

