
@mpipz.bsky.social
with @alaingoriely.bsky.social and Emilia Cozzolino
arxiv.org/abs/2509.06546

with @alaingoriely.bsky.social and Emilia Cozzolino
arxiv.org/abs/2509.06546




www.sciencedirect.com/science/arti...

www.sciencedirect.com/science/arti...

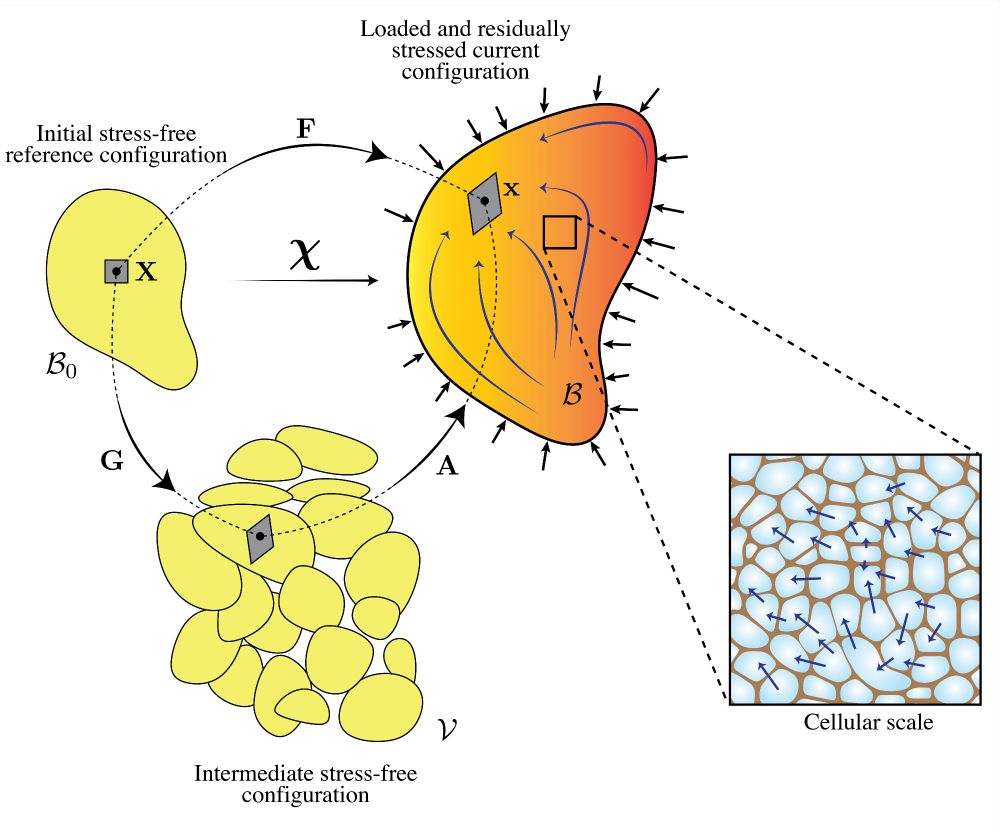



With Ibrahim Cheddadi, we tackled a key challenge: building a field theory of plant morphogenesis, based on fundamental balance laws and capturing cell wall remodelling and water dynamics in tissues🌿💧Check out our paper at www.sciencedirect.com/science/arti...
🧵👇

With Ibrahim Cheddadi, we tackled a key challenge: building a field theory of plant morphogenesis, based on fundamental balance laws and capturing cell wall remodelling and water dynamics in tissues🌿💧Check out our paper at www.sciencedirect.com/science/arti...
🧵👇




