
Website: www.iutzeler.org
See also our previous work the invariant distribution of SGD ( #ICML 2024 ) arxiv.org/abs/2406.09241
See also our previous work the invariant distribution of SGD ( #ICML 2024 ) arxiv.org/abs/2406.09241
💡 Key consequence: Our results explain how the favorable properties of the landscape of NNs drive SGD's convergence
💡 Key consequence: Our results explain how the favorable properties of the landscape of NNs drive SGD's convergence
• When f has no spurious minima → E = 0 → sub-exponential convergence
• Even more: E can be controlled by the depth of spurious minima - shallow minima → small E → fast convergence 🚀
• When f has no spurious minima → E = 0 → sub-exponential convergence
• Even more: E can be controlled by the depth of spurious minima - shallow minima → small E → fast convergence 🚀
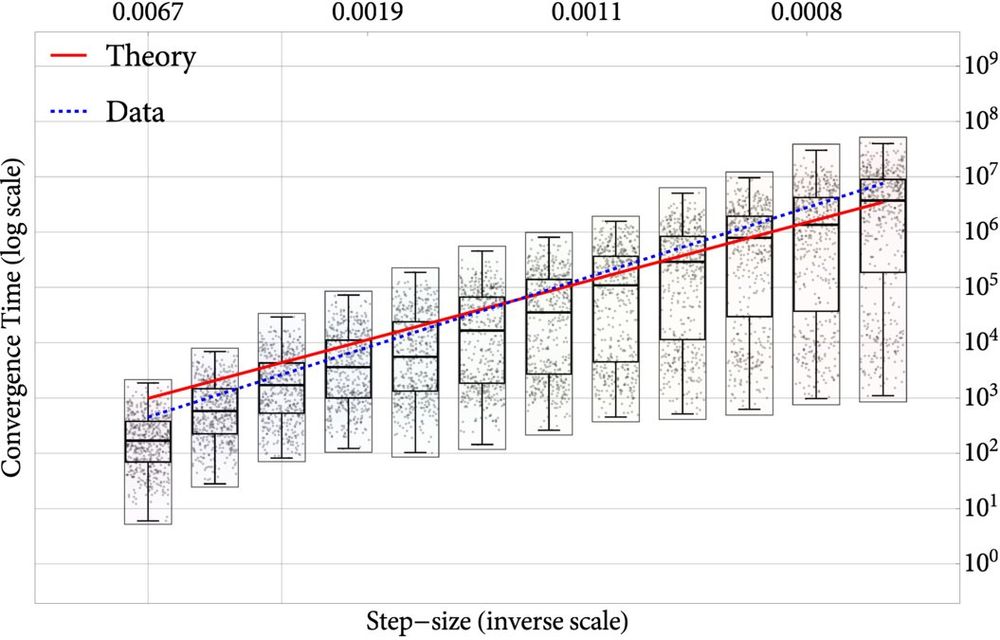
𝔼[τ] ≈ exp(E(x) / η)
where:
• η = (constant) step size of SGD
• E(x) = energy-like function that captures the geometry of the non-convex landscape and the statistics of the noise
𝔼[τ] ≈ exp(E(x) / η)
where:
• η = (constant) step size of SGD
• E(x) = energy-like function that captures the geometry of the non-convex landscape and the statistics of the noise
We ask: for ANY smooth non-convex function, how much time does SGD need to reach the global optimum (escaping all spurious minima along the way)?
We ask: for ANY smooth non-convex function, how much time does SGD need to reach the global optimum (escaping all spurious minima along the way)?

