Florentin Guth
@florentinguth.bsky.social
Postdoc at NYU CDS and Flatiron CCN. Wants to understand why deep learning works.
Finally, we test the manifold hypothesis: what is the local dimensionality around an image? We find that this depends both on the image and the size of the local neighborhood, and there exists images with both large full-dimensional and small low-dimensional neighborhoods.

June 6, 2025 at 10:11 PM
Finally, we test the manifold hypothesis: what is the local dimensionality around an image? We find that this depends both on the image and the size of the local neighborhood, and there exists images with both large full-dimensional and small low-dimensional neighborhoods.
High probability ≠ typicality: very high-probability images are rare. This is not a contradiction: frequency = probability density *multiplied by volume*, and volume is weird in high dimensions! Also, the log probabilities are Gumbel-distributed, and we don't know why!
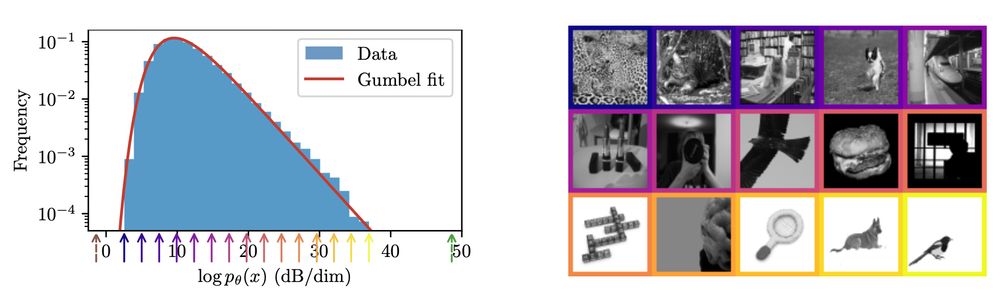
June 6, 2025 at 10:11 PM
High probability ≠ typicality: very high-probability images are rare. This is not a contradiction: frequency = probability density *multiplied by volume*, and volume is weird in high dimensions! Also, the log probabilities are Gumbel-distributed, and we don't know why!
These are the highest and lowest probability images in ImageNet64. An interpretation is that -log2 p(x) is the size in bits of the optimal compression of x: higher probability images are more compressible. Also, the probability ratio between these is 10^14,000! 🤯

June 6, 2025 at 10:11 PM
These are the highest and lowest probability images in ImageNet64. An interpretation is that -log2 p(x) is the size in bits of the optimal compression of x: higher probability images are more compressible. Also, the probability ratio between these is 10^14,000! 🤯
But how do we know our probability model is accurate on real data?
In addition to computing cross-entropy/NLL, we show *strong* generalization: models trained on *disjoint* subsets of the data predict the *same* probabilities if the training set is large enough!
In addition to computing cross-entropy/NLL, we show *strong* generalization: models trained on *disjoint* subsets of the data predict the *same* probabilities if the training set is large enough!

June 6, 2025 at 10:11 PM
But how do we know our probability model is accurate on real data?
In addition to computing cross-entropy/NLL, we show *strong* generalization: models trained on *disjoint* subsets of the data predict the *same* probabilities if the training set is large enough!
In addition to computing cross-entropy/NLL, we show *strong* generalization: models trained on *disjoint* subsets of the data predict the *same* probabilities if the training set is large enough!
We call this approach "dual score matching". The time derivative constrains the learned energy to satisfy the diffusion equation, which enables recovery of accurate and *normalized* log probability values, even in high-dimensional multimodal distributions.

June 6, 2025 at 10:11 PM
We call this approach "dual score matching". The time derivative constrains the learned energy to satisfy the diffusion equation, which enables recovery of accurate and *normalized* log probability values, even in high-dimensional multimodal distributions.
We also propose a simple procedure to obtain good network architectures for the energy U: choose any pre-existing score network s and simply take the inner product with the input image y! We show that this preserves the inductive biases of the base score network: grad_y U ≈ s.

June 6, 2025 at 10:11 PM
We also propose a simple procedure to obtain good network architectures for the energy U: choose any pre-existing score network s and simply take the inner product with the input image y! We show that this preserves the inductive biases of the base score network: grad_y U ≈ s.
How do we train an energy model?
Inspired by diffusion models, we learn the energy of both clean and noisy images along a diffusion. It is optimized via a sum of two score matching objectives, which constrain its derivatives with both the image (space) and the noise level (time).
Inspired by diffusion models, we learn the energy of both clean and noisy images along a diffusion. It is optimized via a sum of two score matching objectives, which constrain its derivatives with both the image (space) and the noise level (time).

June 6, 2025 at 10:11 PM
How do we train an energy model?
Inspired by diffusion models, we learn the energy of both clean and noisy images along a diffusion. It is optimized via a sum of two score matching objectives, which constrain its derivatives with both the image (space) and the noise level (time).
Inspired by diffusion models, we learn the energy of both clean and noisy images along a diffusion. It is optimized via a sum of two score matching objectives, which constrain its derivatives with both the image (space) and the noise level (time).
What is the probability of an image? What do the highest and lowest probability images look like? Do natural images lie on a low-dimensional manifold?
In a new preprint with Zahra Kadkhodaie and @eerosim.bsky.social, we develop a novel energy-based model in order to answer these questions: 🧵
In a new preprint with Zahra Kadkhodaie and @eerosim.bsky.social, we develop a novel energy-based model in order to answer these questions: 🧵

June 6, 2025 at 10:11 PM
What is the probability of an image? What do the highest and lowest probability images look like? Do natural images lie on a low-dimensional manifold?
In a new preprint with Zahra Kadkhodaie and @eerosim.bsky.social, we develop a novel energy-based model in order to answer these questions: 🧵
In a new preprint with Zahra Kadkhodaie and @eerosim.bsky.social, we develop a novel energy-based model in order to answer these questions: 🧵

