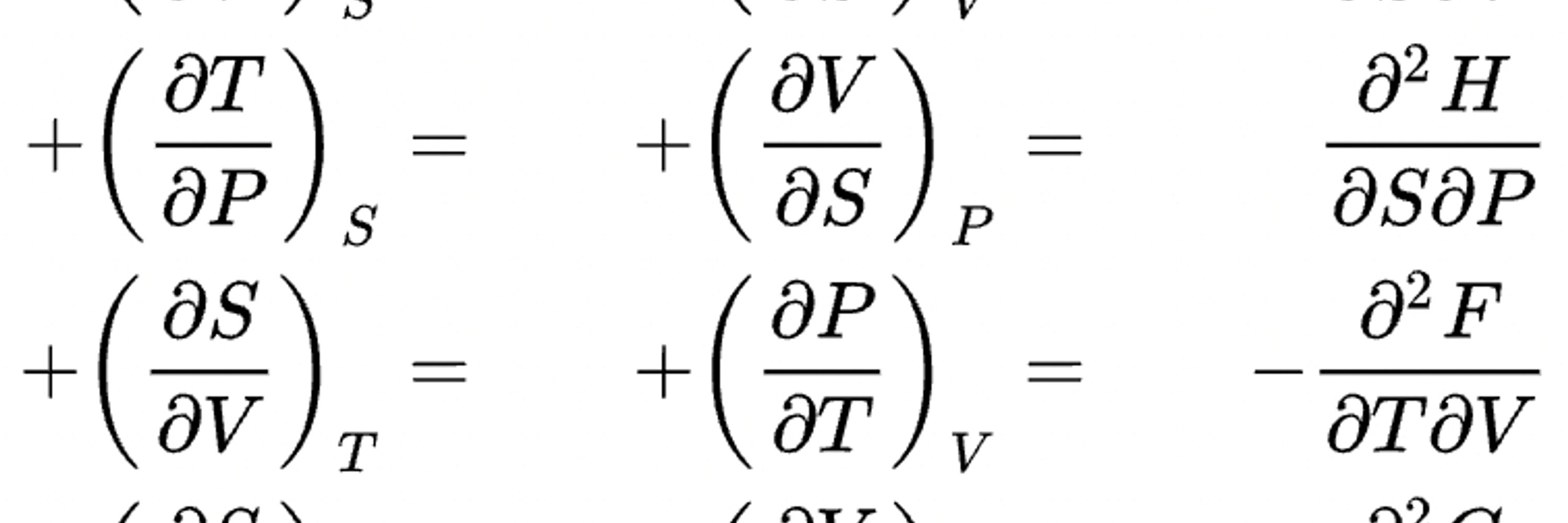
Modelling & Developing Clean Energy Technologies @ Queensland University of Technology





Go - go read them all. Whatever you do, don't read a review; they spoil the effect entirely. You can trust me. Start with 'The Remains of the Day'. That is all.

Go - go read them all. Whatever you do, don't read a review; they spoil the effect entirely. You can trust me. Start with 'The Remains of the Day'. That is all.





Bias occurs when our model is too simple to capture the patterns present in the system. e.g. fitting a line through wavy data.

Bias occurs when our model is too simple to capture the patterns present in the system. e.g. fitting a line through wavy data.
The field is a joy, and full of surprises. Take Double Descent: the unintuitive behaviour which is the mathematical cornerstone allowing massive LLMs to be trained. 🧵

The field is a joy, and full of surprises. Take Double Descent: the unintuitive behaviour which is the mathematical cornerstone allowing massive LLMs to be trained. 🧵
pubs.rsc.org/en/content/a...

pubs.rsc.org/en/content/a...
🧪🔌💡💙📚

🧪🔌💡💙📚




Courtesy @scholargoggler.bsky.social via @sylvaingigan.bsky.social

Courtesy @scholargoggler.bsky.social via @sylvaingigan.bsky.social







