
https://www.annalenakofler.com
#GW10Years
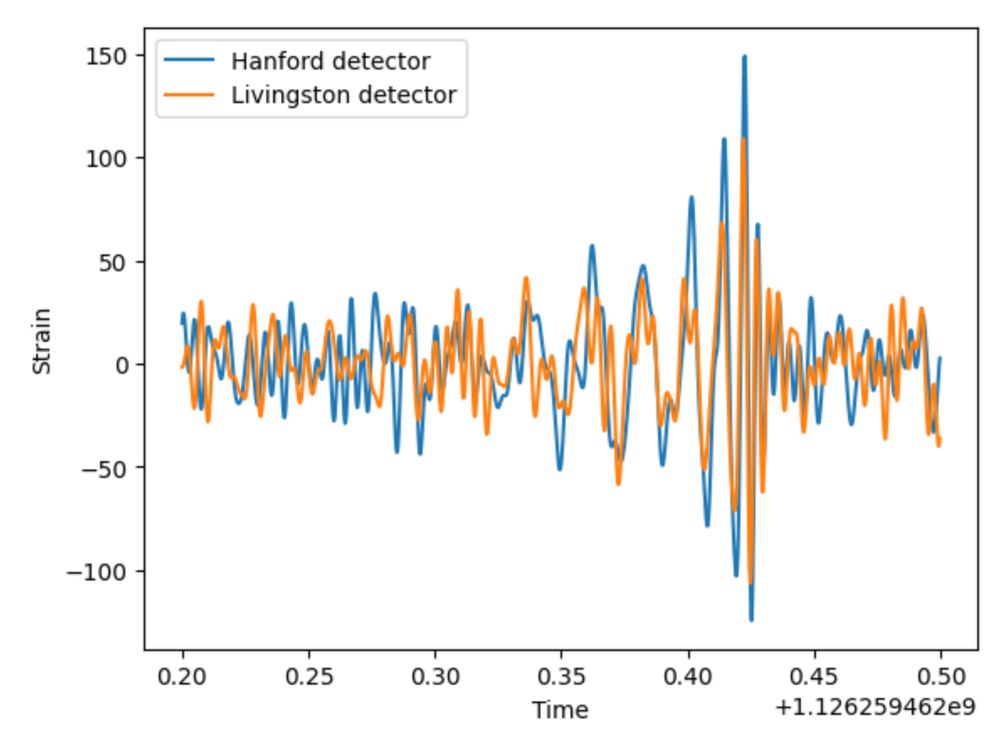
#GW10Years

Astrophysicists are there to help you out: Use pastamarker!

Astrophysicists are there to help you out: Use pastamarker!
1️⃣ FMPE performs as well as nested sampling across different noise levels.
2️⃣ FMPE is faster, more scalable, and achieves higher IS efficiencies.
3️⃣ IS not only corrects inaccuracies but also builds confidence in ML-based retrievals.

1️⃣ FMPE performs as well as nested sampling across different noise levels.
2️⃣ FMPE is faster, more scalable, and achieves higher IS efficiencies.
3️⃣ IS not only corrects inaccuracies but also builds confidence in ML-based retrievals.
1️⃣ FMPE allows greater flexibility in neural architectures compared to NPE and trains ~3x faster! 🚀
2️⃣ IS spots model failures, corrects inaccuracies, and facilitates model comparison via evidence ratios.
3️⃣ Noise-level conditioning enables models to adapt to varying error bars.

1️⃣ FMPE allows greater flexibility in neural architectures compared to NPE and trains ~3x faster! 🚀
2️⃣ IS spots model failures, corrects inaccuracies, and facilitates model comparison via evidence ratios.
3️⃣ Noise-level conditioning enables models to adapt to varying error bars.
We propose a ML-based framework that tackles these challenges:
✨ Flow Matching Posterior Estimation (FMPE): Fast, flexible, and scalable.
✨ Importance Sampling (IS): Verifies ML results, corrects deviations, and computes the Bayesian evidence.

We propose a ML-based framework that tackles these challenges:
✨ Flow Matching Posterior Estimation (FMPE): Fast, flexible, and scalable.
✨ Importance Sampling (IS): Verifies ML results, corrects deviations, and computes the Bayesian evidence.
ML methods like Neural Posterior Estimation (NPE) have shown promise for atmospheric retrieval. But they come with challenges:
1️⃣ Ensuring reliability and accuracy of the estimated posteriors.
2️⃣ Adapting to different noise levels and models on the fly.

ML methods like Neural Posterior Estimation (NPE) have shown promise for atmospheric retrieval. But they come with challenges:
1️⃣ Ensuring reliability and accuracy of the estimated posteriors.
2️⃣ Adapting to different noise levels and models on the fly.
To understand how exoplanets form, evolve, and whether they might harbor life, we need to infer their atmospheric properties from observed emission spectra. 🌈
Traditionally, this is done with Bayesian methods like nested sampling, but these are computationally expensive. 💻💰

To understand how exoplanets form, evolve, and whether they might harbor life, we need to infer their atmospheric properties from observed emission spectra. 🌈
Traditionally, this is done with Bayesian methods like nested sampling, but these are computationally expensive. 💻💰
The latest work by my amazing collaborator @timothygebhard.bsky.social introduces Flow Matching Posterior Estimation for atmospheric retrieval. 🚀🧵👇
#AI #MachineLearning #Physics #Astronomy #AcademicSky

The latest work by my amazing collaborator @timothygebhard.bsky.social introduces Flow Matching Posterior Estimation for atmospheric retrieval. 🚀🧵👇
#AI #MachineLearning #Physics #Astronomy #AcademicSky


In our experiments:
1️⃣ FAB outperformed traditional methods in high dimensions.
2️⃣ Achieved higher sampling efficiency with fewer evaluations of the target density.
3️⃣ No need for costly pre-generated training data—saving time and compute!
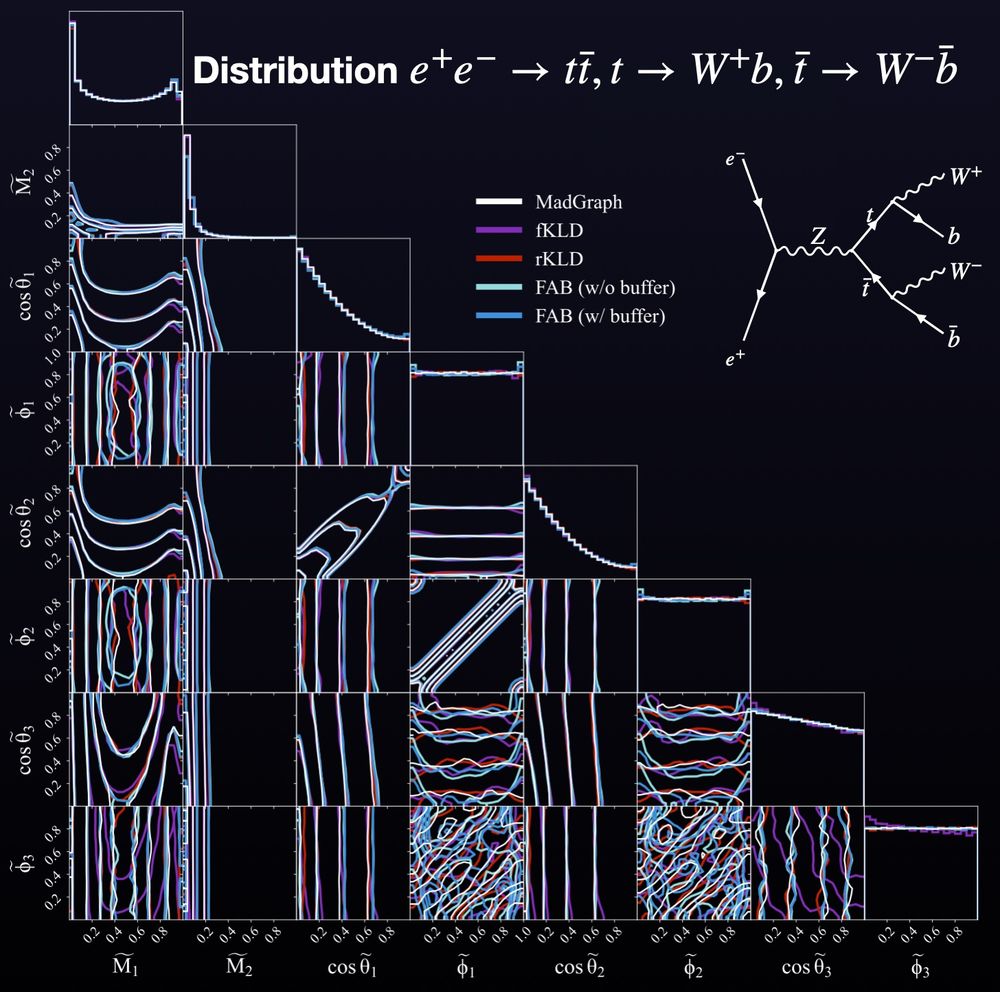
In our experiments:
1️⃣ FAB outperformed traditional methods in high dimensions.
2️⃣ Achieved higher sampling efficiency with fewer evaluations of the target density.
3️⃣ No need for costly pre-generated training data—saving time and compute!
To accelerate sampling from matrix elements, surrogate models (like normalizing flows) are used to approximate these distributions. But how can we train normalizing flows in the best way? We compare different training approaches, including FAB. 🌟

To accelerate sampling from matrix elements, surrogate models (like normalizing flows) are used to approximate these distributions. But how can we train normalizing flows in the best way? We compare different training approaches, including FAB. 🌟
The analysis of high-energy physics (HEP) data relies on large amounts of simulated samples drawn from analytically tractable distributions ('matrix elements'). Keeping up with the increasing demand of simulated data is impossible with current methods.

The analysis of high-energy physics (HEP) data relies on large amounts of simulated samples drawn from analytically tractable distributions ('matrix elements'). Keeping up with the increasing demand of simulated data is impossible with current methods.
We explore the intersection of high-energy physics and machine learning. What's the challenge we’re targeting, and why does it matter? Let's dive in! 🧵👇
🚀 #AI #MachineLearning #Physics #ML4PS #NeurIPS #AcademicSky
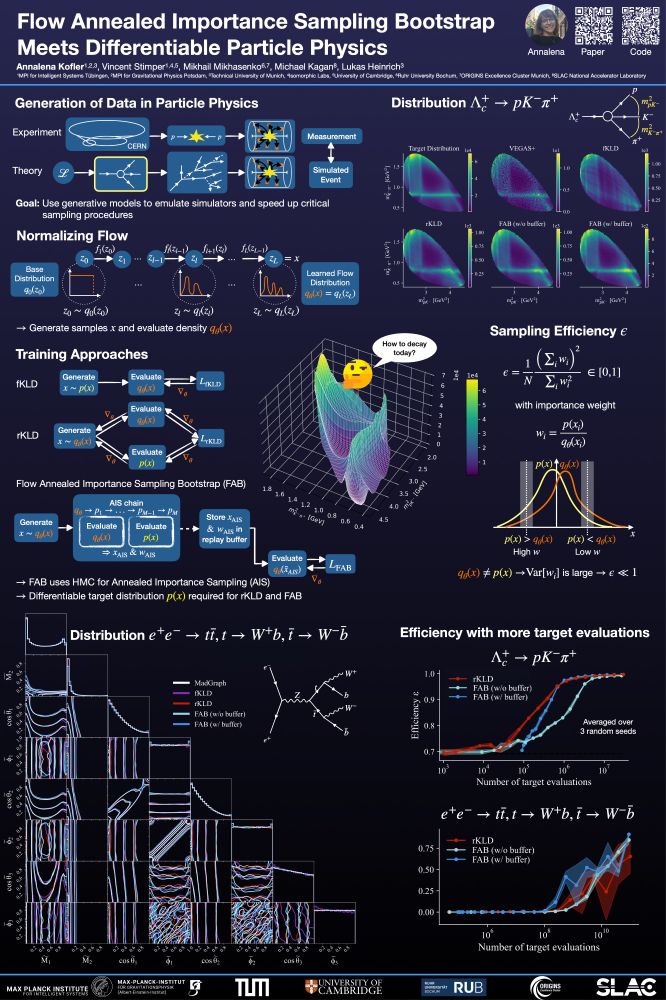
We explore the intersection of high-energy physics and machine learning. What's the challenge we’re targeting, and why does it matter? Let's dive in! 🧵👇
🚀 #AI #MachineLearning #Physics #ML4PS #NeurIPS #AcademicSky




