
and Gresham Professor of Geometry at Gresham College, London
[5/n]

[5/n]
[4/n]

[4/n]
All three statements below are incorrect.
[3/n]

All three statements below are incorrect.
[3/n]
All three statements below are incorrect.
[2/n]

All three statements below are incorrect.
[2/n]
academic.oup.com/pnasnexus/ar...

academic.oup.com/pnasnexus/ar...
(started in 1670).
With parents around, it is a good day to check the almost universal law that boys are taller than their mother.

(started in 1670).
With parents around, it is a good day to check the almost universal law that boys are taller than their mother.

Do read the original paper!
www.nature.com/articles/s41...

Do read the original paper!
www.nature.com/articles/s41...
Actually, no verified image from his lifetime can be confirmed as authentic.
www.academie-sciences-lettres-toulouse.fr/wp-content/u...
“.. rare, if not nonexistent, are those (portraits) we know to be authentic…”

Actually, no verified image from his lifetime can be confirmed as authentic.
www.academie-sciences-lettres-toulouse.fr/wp-content/u...
“.. rare, if not nonexistent, are those (portraits) we know to be authentic…”
Here is a short list of famous mathematicians/scientists with no known portrait (AFAIK):
Pythagoras (c. 570–495 BCE)
Zeno of Elea (c. 490–430 BCE)
Al-Khwarizmi (c. 780–850)
Nicole Oresme (c. 1320–1382)
1/2

Here is a short list of famous mathematicians/scientists with no known portrait (AFAIK):
Pythagoras (c. 570–495 BCE)
Zeno of Elea (c. 490–430 BCE)
Al-Khwarizmi (c. 780–850)
Nicole Oresme (c. 1320–1382)
1/2

royalsocietypublishing.org/doi/epdf/10....
We identify situations where disease initiation can be caused by focal hypoperfusion following vascular injury.
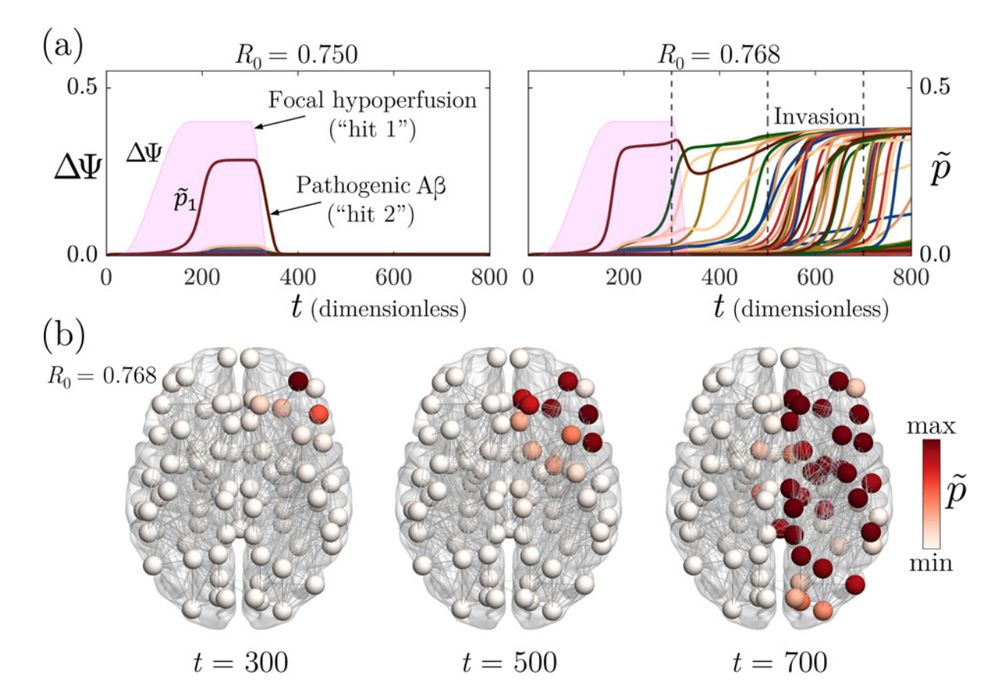
royalsocietypublishing.org/doi/epdf/10....
We identify situations where disease initiation can be caused by focal hypoperfusion following vascular injury.

Now in Polish (my father’s mother tongue, he would have approved).

Now in Polish (my father’s mother tongue, he would have approved).
Beware: the pellet with the poison is in the flagon with the dragon

Beware: the pellet with the poison is in the flagon with the dragon
In this collaboration with José A. Sanz-Herrera, we show that this inverse problem can be solved.
authors.elsevier.com/a/1kiv357ZkC...

In this collaboration with José A. Sanz-Herrera, we show that this inverse problem can be solved.
authors.elsevier.com/a/1kiv357ZkC...

Stop by his house when in Oxford.
www.college-de-france.fr/fr/agenda/co...


Stop by his house when in Oxford.
www.college-de-france.fr/fr/agenda/co...
A typical value cited in the literature is 86 billion.
However, as I argue in this essay, the data does not justify this number and we do not have yet a satisfactory answer
academic.oup.com/brain/advanc...
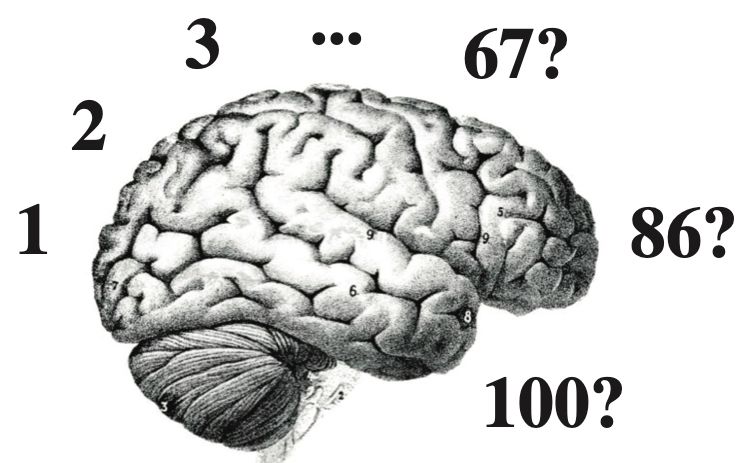
A typical value cited in the literature is 86 billion.
However, as I argue in this essay, the data does not justify this number and we do not have yet a satisfactory answer
academic.oup.com/brain/advanc...
They are all part of a new space-filling family!
Find out more about the beautiful geometry of cells in this paper
arxiv.org/pdf/2412.04491

They are all part of a new space-filling family!
Find out more about the beautiful geometry of cells in this paper
arxiv.org/pdf/2412.04491
Here is the paper
www.pnas.org/doi/10.1073/...

Here is the paper
www.pnas.org/doi/10.1073/...

