
abeljansma.nl
This led to a really fun collaboration, and a new approach to “engineer emergence”.
Erik just published an overview of the ideas, goals, and dreams:

This led to a really fun collaboration, and a new approach to “engineer emergence”.
Erik just published an overview of the ideas, goals, and dreams:



Classical Shapley values only work for real-valued functions on power sets of players (or lattices).
We generalise them even beyond posets to
✅vector/group-valued fns
✅weighted directed acyclic multigraphs
, and prove uniqueness!

Classical Shapley values only work for real-valued functions on power sets of players (or lattices).
We generalise them even beyond posets to
✅vector/group-valued fns
✅weighted directed acyclic multigraphs
, and prove uniqueness!
We reinterpret Shapley values as projection operators: a recursive re-attribution of higher-order synergy to lower-order parts.
This turns Shapley values into a general projection framework for hierarchical structure, valid far beyond game theory.

We reinterpret Shapley values as projection operators: a recursive re-attribution of higher-order synergy to lower-order parts.
This turns Shapley values into a general projection framework for hierarchical structure, valid far beyond game theory.
If Shapley values are truly general, we should be able to express them for any Möbius inversion/higher-order structure.

If Shapley values are truly general, we should be able to express them for any Möbius inversion/higher-order structure.

It includes a new analysis to show that LLM semantics can be decomposed: the negativity of "horribly bad" is redundantly encoded in the two words, whereas "not bad" has synergistic semantics (i.e. negation):

It includes a new analysis to show that LLM semantics can be decomposed: the negativity of "horribly bad" is redundantly encoded in the two words, whereas "not bad" has synergistic semantics (i.e. negation):





I tested this on
- Logic gates
- Cellular automata
- Chemical reaction networks.

I tested this on
- Logic gates
- Cellular automata
- Chemical reaction networks.
It's pretty complicated, but with
@frosas.bsky.social
and @PedroMediano we recently calculated the ‘fast Möbius transform’ for it: arxiv.org/abs/2410.06224
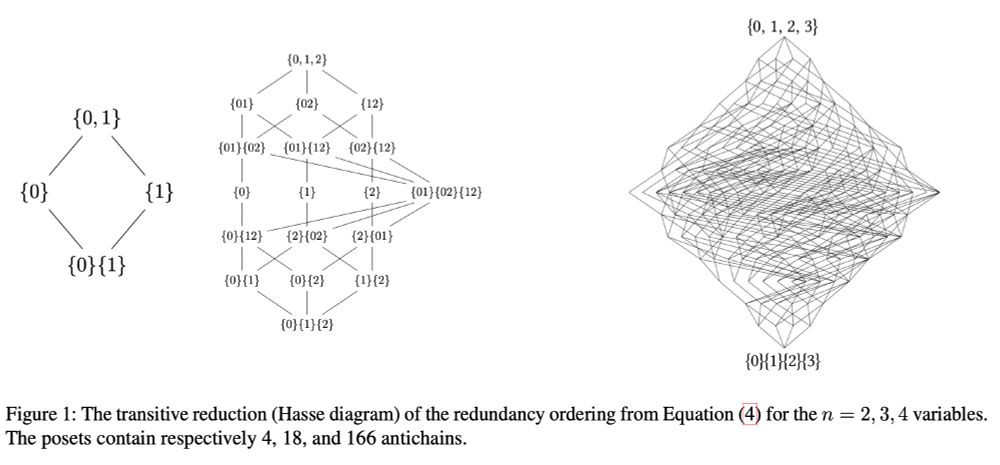
It's pretty complicated, but with
@frosas.bsky.social
and @PedroMediano we recently calculated the ‘fast Möbius transform’ for it: arxiv.org/abs/2410.06224
@yudapearl's do-calculus:

@yudapearl's do-calculus:
I tested this on
- Logic gates
- Cellular automata
- Chemical reaction networks.

I tested this on
- Logic gates
- Cellular automata
- Chemical reaction networks.
It's pretty complicated, but with @frosas.bsky.social and @PedroMediano we recently calculated the ‘fast Möbius transform’ for it: arxiv.org/abs/2410.06224

It's pretty complicated, but with @frosas.bsky.social and @PedroMediano we recently calculated the ‘fast Möbius transform’ for it: arxiv.org/abs/2410.06224
@yudapearl's do-calculus:

@yudapearl's do-calculus:
Now in 15 months, AIs have gone from random guessing to expert level.

Now in 15 months, AIs have gone from random guessing to expert level.




