Join us at TPM @auai.org #UAI2025 and show how to build #neurosymbolic / #probabilistic AI that is both fast and trustworthy!
Join us at TPM @auai.org #UAI2025 and show how to build #neurosymbolic / #probabilistic AI that is both fast and trustworthy!
TLDR;
To estimate µ = E_p[f(θ)] with SNIS, instead of doing MCMC on p(θ) or learning a parametric q(θ), we try MCMC directly on p(θ)| f(θ)-µ | (variance-minimizing proposal).
arxiv.org/abs/2505.00372

TLDR;
To estimate µ = E_p[f(θ)] with SNIS, instead of doing MCMC on p(θ) or learning a parametric q(θ), we try MCMC directly on p(θ)| f(θ)-µ | (variance-minimizing proposal).
arxiv.org/abs/2505.00372
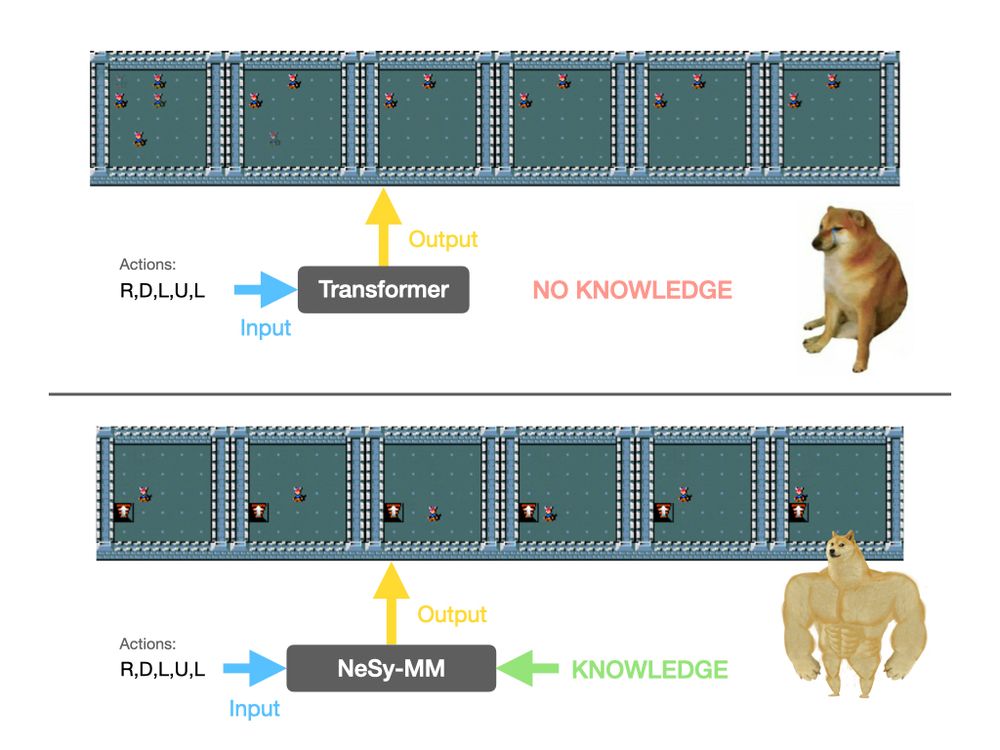
Super interesting topic combining DL + NeSy + HMMs! Keep an eye on Lennert's future works!

Super interesting topic combining DL + NeSy + HMMs! Keep an eye on Lennert's future works!
Submit your works on:
- fast and #reliable inference
- #circuits and #tensor #networks
- normalizing #flows
- scaling #NeSy #AI
...& more!
🕓 deadline: 23/05/25
👉 tractable-probabilistic-modeling.github.io/tpm2025/

📜 Paper: arxiv.org/pdf/2412.13023
💻 Code: github.com/ML-KULeuven/...
🧵⬇️
📜 Paper: arxiv.org/pdf/2412.13023
💻 Code: github.com/ML-KULeuven/...
🧵⬇️
We use recursive integer arithmetic to express combinatorial problems and add uncertainty. Inference can be massively accelerated with tensors and the FFT. 🚀
We use recursive integer arithmetic to express combinatorial problems and add uncertainty. Inference can be massively accelerated with tensors and the FFT. 🚀

