www.desmos.com/geometry/why...
#iTeachMath #MathSky
www.desmos.com/geometry/why...
#iTeachMath #MathSky
classroom.amplify.com/activity/690...
#iTeachMath #MathSky
classroom.amplify.com/activity/690...
#iTeachMath #MathSky
www.desmos.com/3d/fiv5gnltdl
(The option to have translucent surfaces doesn't save with the graph itself, so needs to be re-toggled on. It's important for seeing the full curves)
#MathSky #iTeachMath
www.desmos.com/3d/fiv5gnltdl
(The option to have translucent surfaces doesn't save with the graph itself, so needs to be re-toggled on. It's important for seeing the full curves)
#MathSky #iTeachMath

Here's the graph:
www.desmos.com/3d/hadt9rebbe
They recently enabled colouring a surface using functions, so far only in 3D grapher. Side-effect: allows complex domain colouring, using 3D tool as a 2D one! #iTeachMath #MathSky
Here's the graph:
www.desmos.com/3d/hadt9rebbe
They recently enabled colouring a surface using functions, so far only in 3D grapher. Side-effect: allows complex domain colouring, using 3D tool as a 2D one! #iTeachMath #MathSky
www.desmos.com/geometry/wgp...
#iTeachMath #MathSky
www.desmos.com/geometry/wgp...
#iTeachMath #MathSky
www.desmos.com/geometry/x46...
#iTeachMath
www.desmos.com/geometry/x46...
#iTeachMath
Does this QR code work for your phone? It does with mine. It should take you to my website.

Does this QR code work for your phone? It does with mine. It should take you to my website.

classroom.amplify.com/activity/68c...
For a really great intro to how this relates to group theory, see this by @stevenstrogatz.com archive.nytimes.com/opinionator....
classroom.amplify.com/activity/68c...
For a really great intro to how this relates to group theory, see this by @stevenstrogatz.com archive.nytimes.com/opinionator....
It’s a nicely designed light, but it’s not a hexagon! #

It’s a nicely designed light, but it’s not a hexagon! #
en.wikipedia.org/wiki/Brianch...
en.wikipedia.org/wiki/Brianch...
I’m curious about that point, and how to show that the lines are concurrent there.

I’m curious about that point, and how to show that the lines are concurrent there.
Fun to drag the tangent points around and see how the concurrency remains. Try it with hyperbolas and a parabola too. It also works!

Fun to drag the tangent points around and see how the concurrency remains. Try it with hyperbolas and a parabola too. It also works!
I was messing around with conics and ran across your GeoGebra inscribed one. I’m curious: do you happen to know what the point H is called, and how one might prove that the tangent-to-vertex lines are concurrent there? Thanks!
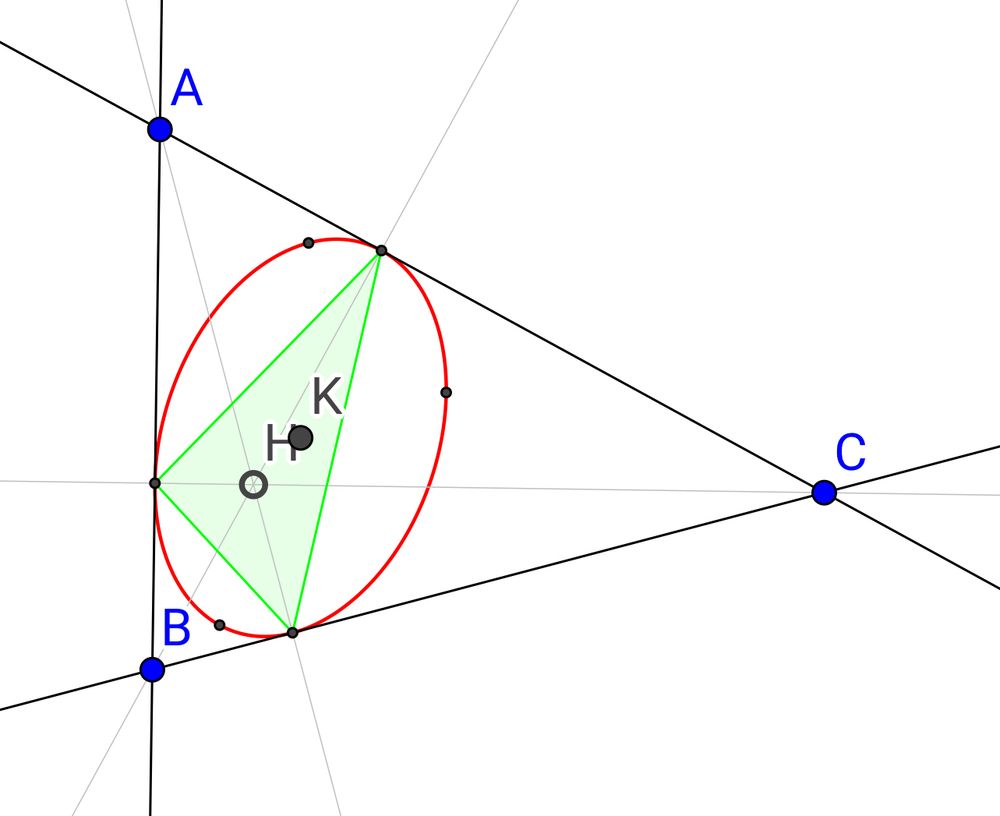
I was messing around with conics and ran across your GeoGebra inscribed one. I’m curious: do you happen to know what the point H is called, and how one might prove that the tangent-to-vertex lines are concurrent there? Thanks!
www.desmos.com/calculator/m...
www.desmos.com/calculator/m...

www.desmos.com/calculator/k...
www.desmos.com/calculator/k...
www.desmos.com/geometry/863...
www.desmos.com/geometry/863...
openprocessing.org/sketch/2664137
openprocessing.org/sketch/2664137
Your suggestion prompted me to try repeating that process a couple of times, simply because it would look pretty:
www.desmos.com/geometry/uns...
Your suggestion prompted me to try repeating that process a couple of times, simply because it would look pretty:
www.desmos.com/geometry/uns...
www.desmos.com/geometry/n0a...
www.desmos.com/geometry/n0a...

