[8/8] Curious to learn more? Check the link in the first post for the whole story ☝️
Lastly, huge kudos to Julian Voits and @ulrichschwarz.bsky.social, who independently reached similar conclusions: arxiv.org/html/2403.17... (soon in PRX Life).

[7/8] Our model, a step toward a deeper mechanistic understanding of how biological processes scale with temperature, offers an alternative perspective that embraces the underlying complexity of biochemical regulation.

[6/8] Our scaling equation – a quadratic-exponential function with single-exponential deviations at extremes – fits 100+ temperature-response curves across traits and taxa, offering a sound estimate of mean activation energy.

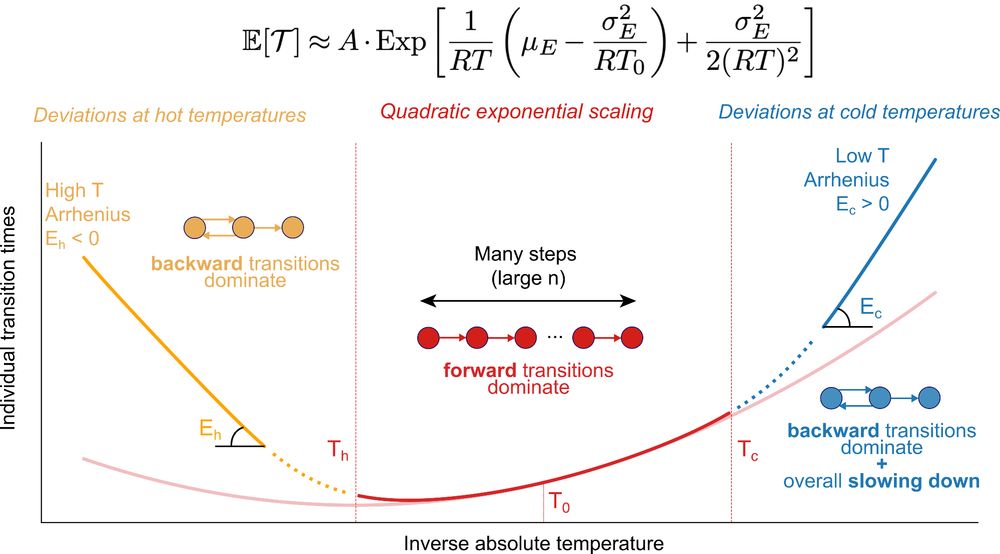
[5/8] At temperature extremes, timing deviates from the quadratic-exponential law. It becomes dominated by the slowest rate-limiting step, where forward transitions turn slower than backward ones – effectively trapping the process in a loop.

[4/8] Interestingly, this quadratic-exponential behavior holds within a range around the reference temperature, where forward transitions dominate and averaging applies.

[3/8] The completion time of such multi-step processes, i.e., reaching step n from step 1, was found to follow a quadratic-exponential function of inverse temperature. This scaling, seen in experiments, naturally emerges from averaging over many independent intermediate steps.

[2/8] Our model is relatively straightforward: a cascade of n (reversible) Markov jump processes, each transition rate following Arrhenius-like temperature scaling, with forward transitions favored near a reference temperature.

[1/8] Biological processes are governed by complex biochemical networks – far beyond single reactions – and often form multi-step transition cascades. Together with Simen Jacobs, Federico Vazquez, and @lendertgelens.bsky.social, we show that modeling these as Markov chains has striking consequences.

Congratulations, Jan! Happy to see it out; it’ll be a nice read this weekend :)