Postdoctoral Research Scientist @ ETH Zürich
↳ https://matteosaponati.github.io
shamelessly adding here that many different types of STDP come about from minimizing a prediction of the future loss function with spikes :)
hopefully another case of successful predictions.
www.nature.com/articles/s41...

shamelessly adding here that many different types of STDP come about from minimizing a prediction of the future loss function with spikes :)
hopefully another case of successful predictions.
www.nature.com/articles/s41...
cheers 💜

cheers 💜
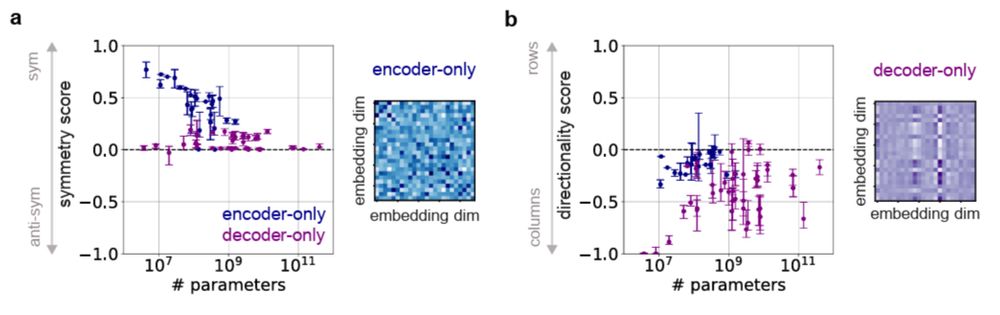
- Self-attention matrices in Transformers show universal structural differences based on training.
- Bidirectional models → Symmetric self-attention
- Autoregressive models → Directional, column-dominant
- Using symmetry as an inductive bias improves training.
⬇️
- Self-attention matrices in Transformers show universal structural differences based on training.
- Bidirectional models → Symmetric self-attention
- Autoregressive models → Directional, column-dominant
- Using symmetry as an inductive bias improves training.
⬇️
- Initializing self-attention matrices symmetrically improves training efficiency for bidirectional models, leading to faster convergence.
This suggest that imposing structures at initialization can enhance training dynamics.
⬇️

- Initializing self-attention matrices symmetrically improves training efficiency for bidirectional models, leading to faster convergence.
This suggest that imposing structures at initialization can enhance training dynamics.
⬇️
- ModernBERT, GPT, LLaMA3, Mistral, etc
- Text, vision, and audio models
- Different model sizes, and architectures
⬇️
- ModernBERT, GPT, LLaMA3, Mistral, etc
- Text, vision, and audio models
- Different model sizes, and architectures
⬇️
- Bidirectional training (BERT-style) induces symmetric self-attention structures.
- Autoregressive training (GPT-style) induces directional structures with column dominance.
⬇️
- Bidirectional training (BERT-style) induces symmetric self-attention structures.
- Autoregressive training (GPT-style) induces directional structures with column dominance.
⬇️
We introduce a mathematical framework to study these matrices and uncover fundamental differences in how they are updated during gradient descent.
⬇️
We introduce a mathematical framework to study these matrices and uncover fundamental differences in how they are updated during gradient descent.
⬇️

