and @ENSdeLyon
Machine Learning, Python and Optimization
Applying Jacobian regularization, we recover effects seen previously on perturbed denoisers (drift vs noise)

Applying Jacobian regularization, we recover effects seen previously on perturbed denoisers (drift vs noise)


Are FM & diffusion models nothing else than denoisers at every noise level?
In theory yes, *if trained optimally*. But in practice, do all noise level equally matter?
with @annegnx.bsky.social, S Martin & R Gribonval
Are FM & diffusion models nothing else than denoisers at every noise level?
In theory yes, *if trained optimally*. But in practice, do all noise level equally matter?
with @annegnx.bsky.social, S Martin & R Gribonval


@skate-the-apple.bsky.social


@skate-the-apple.bsky.social
arxiv.org/abs/2506.03719

arxiv.org/abs/2506.03719
Broadcast available at gdr-iasis.cnrs.fr/reunions/mod...


Broadcast available at gdr-iasis.cnrs.fr/reunions/mod...


The inductive bias of the neural network prevents from perfectly learning u* and overfitting.
In particular neural networks fail to learn the velocity field for two particular time values.
See the paper for a finer analysis 😀

The inductive bias of the neural network prevents from perfectly learning u* and overfitting.
In particular neural networks fail to learn the velocity field for two particular time values.
See the paper for a finer analysis 😀
On the opposite, removing target stochasticity helps generalizing faster.
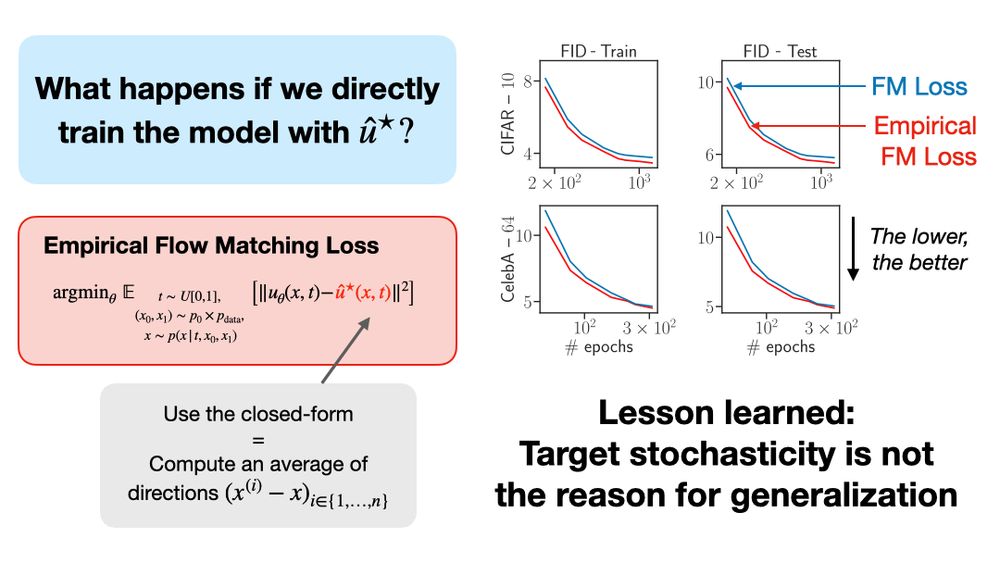
On the opposite, removing target stochasticity helps generalizing faster.
An hypothesis to explain this paradox is target stochasticity: FM targets the conditional velocity field ie only a stochastic approximation of the full velocity field u*
*We refute this hypothesis*: very early, the approximation almost equals u*
An hypothesis to explain this paradox is target stochasticity: FM targets the conditional velocity field ie only a stochastic approximation of the full velocity field u*
*We refute this hypothesis*: very early, the approximation almost equals u*
🤯 Why does flow matching generalize? Did you know that the flow matching target you're trying to learn *can only generate training points*?
w @quentinbertrand.bsky.social @annegnx.bsky.social @remiemonet.bsky.social 👇👇👇
🤯 Why does flow matching generalize? Did you know that the flow matching target you're trying to learn *can only generate training points*?
w @quentinbertrand.bsky.social @annegnx.bsky.social @remiemonet.bsky.social 👇👇👇
Our material is publicly available !!! github.com/QB3/SenHubIA...
ensdelyon.bsky.social


Our material is publicly available !!! github.com/QB3/SenHubIA...
ensdelyon.bsky.social
The illustrations are much nicer in the blog post, go read it !
👉👉 dl.heeere.com/conditional-... 👈👈

The illustrations are much nicer in the blog post, go read it !
👉👉 dl.heeere.com/conditional-... 👈👈
The key to learn it is to introduce a conditioning random variable, breaking the pb into smaller ones that have closed form solutions.
Here's the magic: the small problems can be used to solve the original one!

The key to learn it is to introduce a conditioning random variable, breaking the pb into smaller ones that have closed form solutions.
Here's the magic: the small problems can be used to solve the original one!
2 benefits:
- no need to compute likelihoods nor solve ODE in training
- makes the problem better posed by defining a *unique sequence of densities* from base to target
2 benefits:
- no need to compute likelihoods nor solve ODE in training
- makes the problem better posed by defining a *unique sequence of densities* from base to target
We got this idea after their cool work on improving Plug and Play with FM: arxiv.org/abs/2410.02423
We got this idea after their cool work on improving Plug and Play with FM: arxiv.org/abs/2410.02423
it is possible to embed any cloud of N points from R^d into R^k without distorting their respective distances too much, provided k is not too small (independently of d!)
Better: any random Gaussian embedding works with high proba!
it is possible to embed any cloud of N points from R^d into R^k without distorting their respective distances too much, provided k is not too small (independently of d!)
Better: any random Gaussian embedding works with high proba!
Higher conditioning => harder to minimize the function
Gradient Descent gets faster on function with decreasing conditioning L/mu 👇
Higher conditioning => harder to minimize the function
Gradient Descent gets faster on function with decreasing conditioning L/mu 👇
mathurinm.github.io/hutchinson/

mathurinm.github.io/hutchinson/
1°: Two equivalent views on PCA: maximize the variance of the projected data, or minimize the reconstruction error
1°: Two equivalent views on PCA: maximize the variance of the projected data, or minimize the reconstruction error

