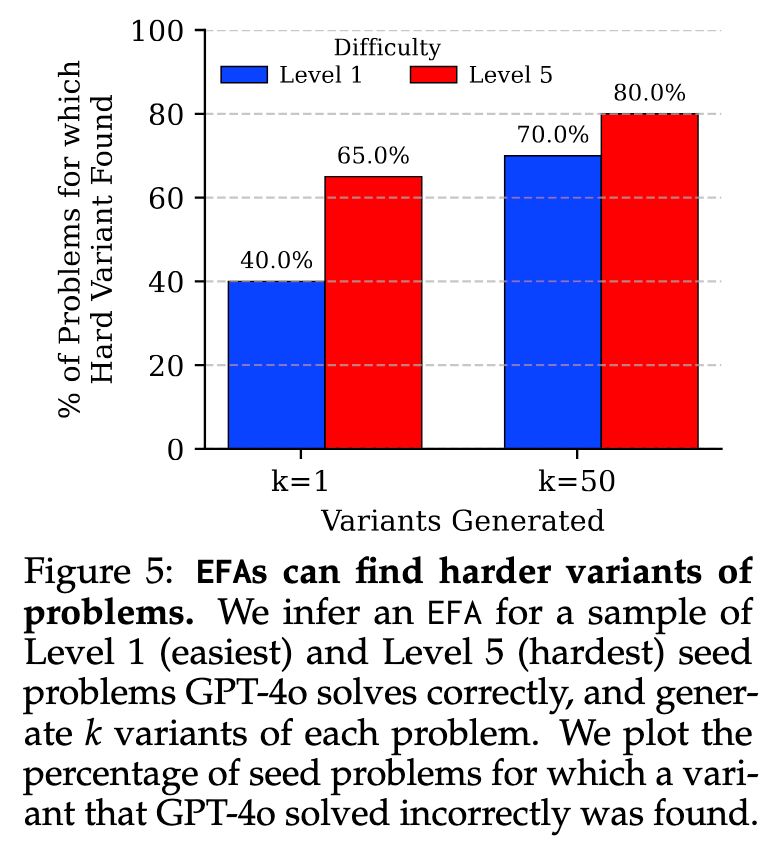
EFAs can be used for adversarial search to find harder problem variants. This has some interesting potential uses, such as finding fresh problems for online RL or identifying gaps / inconsistencies in a model’s reasoning ability. We can find variants of even Level 1 problems (GPT-4o) solves wrong.

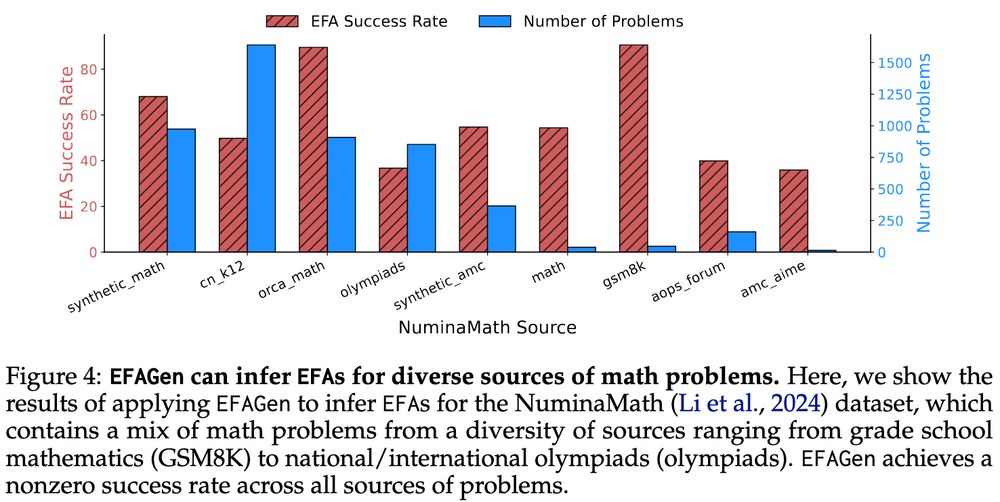
EFAGen can infer EFAs for diverse sources of math data.

We demonstrate this by inferring EFAs on the NuminaMath dataset, which includes problems ranging from grade school to olympiad level problems. EFAGen can successfully infer EFAs for all math sources in NuminaMath, even olympiad-level problems.

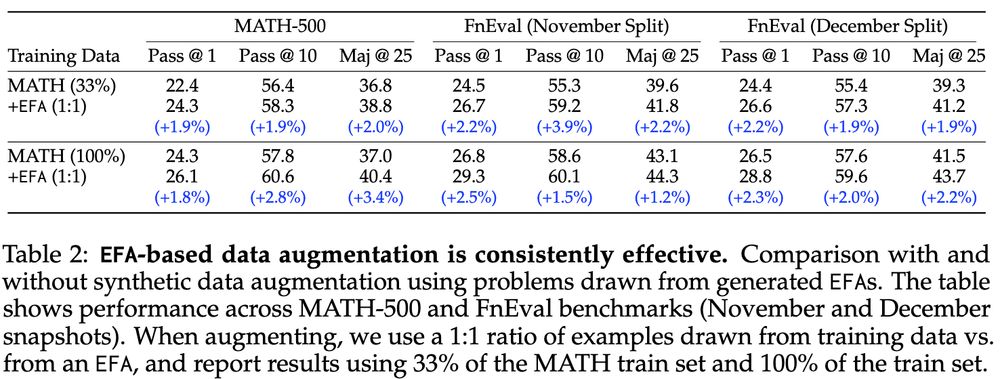
EFAs are effective at augmenting training data.

Getting high-quality math data is expensive. EFAGen offers a way to improve upon existing math training data by generating problem variants through EFAs. EFA-based augmentation leads to consistent improvements across all evaluation metrics.

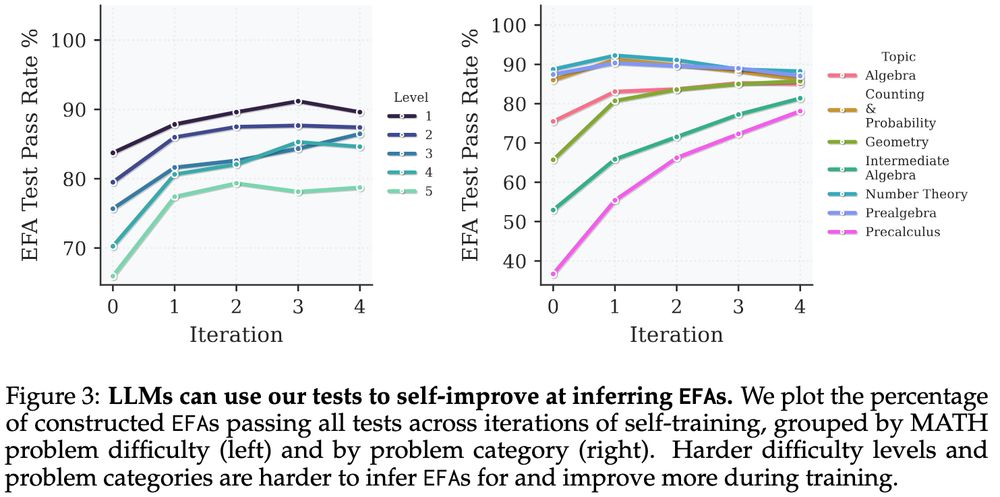
LMs can self-improve at inferring EFAs with execution feedback!

We self-train Llama-3.1-8B-Instruct with rejection finetuning using our derived unit tests as a verifiable reward signal and see substantial improvements in the model’s ability to infer EFAs, especially on harder problems.

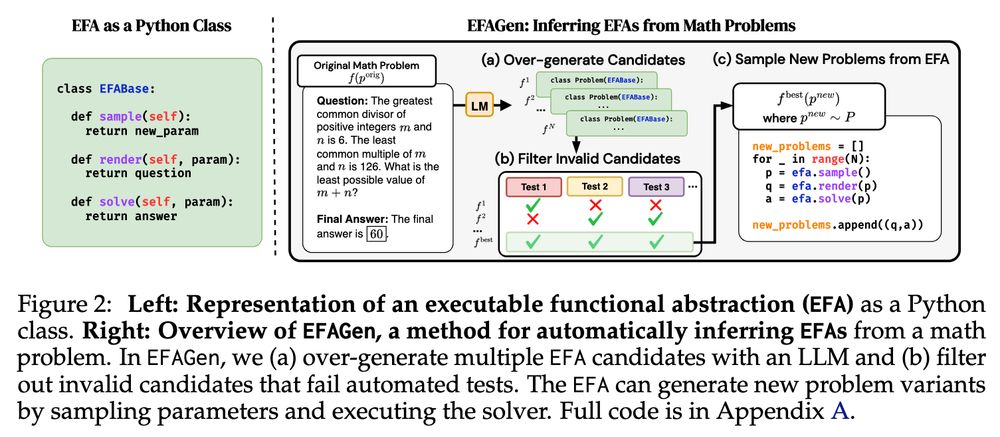
Key Insight💡: We formalize properties any valid EFA must possess as unit tests and treat EFA inference as a program synthesis task that we can apply test-time search to.

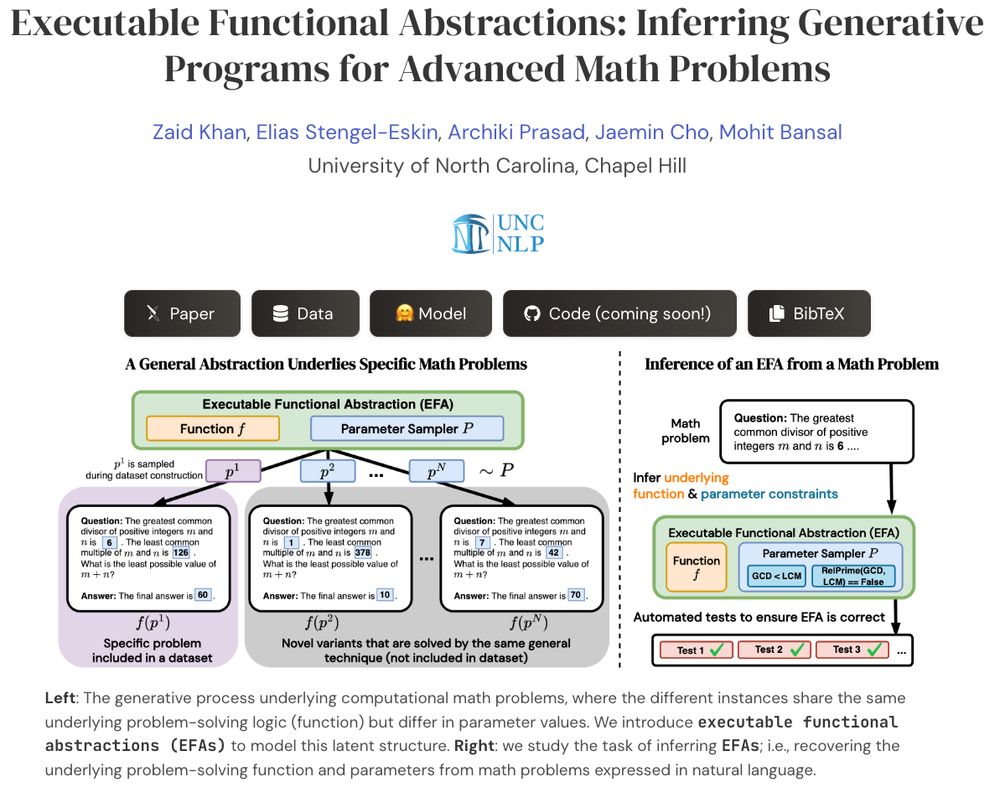
What if we could transform advanced math problems into abstract programs that can generate endless, verifiable problem variants?

Presenting EFAGen, which automatically transforms static advanced math problems into their corresponding executable functional abstractions (EFAs).
🧵👇