
Christian Bick
@bickmath.bsky.social
Dynamics, Networks, and Dynamics. Based at VU Amsterdam but also roaming around Exeter, Munich, and Oxford (family permitting). Personal webpage at https://www.math.vu.nl/~bick/ and more social media at https://linktr.ee/cbick.
A summary of the results are now also part of a @oxfordmathematics.bsky.social Research Case Study: www.maths.ox.ac.uk/node/74552
Reducing the dimensions of adaptive networks - a case study by Christian Bick | Mathematical Institute
www.maths.ox.ac.uk
November 4, 2025 at 7:52 AM
A summary of the results are now also part of a @oxfordmathematics.bsky.social Research Case Study: www.maths.ox.ac.uk/node/74552
The nice summary "Reducing the dimensions of adaptive networks" for a broader audience was published alongside the paper at doi.org/10.1063/10.0...
Reducing the dimensions of adaptive networks
Framework for decreasing the dimensionality of complex systems facilitates analysis of complexity.
doi.org
October 28, 2025 at 4:01 PM
The nice summary "Reducing the dimensions of adaptive networks" for a broader audience was published alongside the paper at doi.org/10.1063/10.0...
This motivates new mathematical insights into the multiple time scale dynamics of adaptive networks. And opens up questions how constraints and adaptive dependency is realized in real world adaptive networks.
October 28, 2025 at 4:01 PM
This motivates new mathematical insights into the multiple time scale dynamics of adaptive networks. And opens up questions how constraints and adaptive dependency is realized in real world adaptive networks.
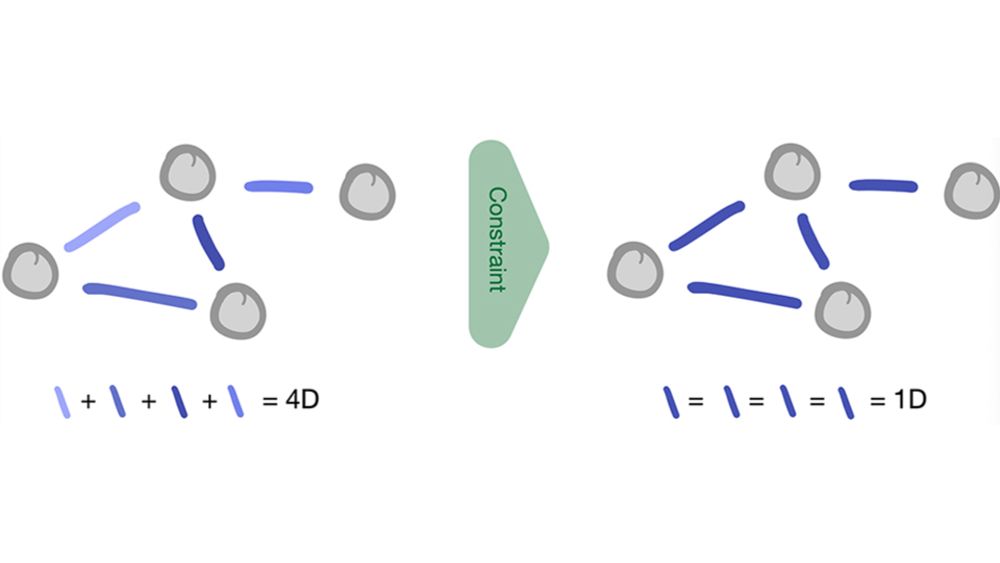
We introduce constraints to the adaptive dynamics as a way to reduce dimensionality. These may be intrinsic, for example, if the adaptation rule is nondirectional. Or they may be forced by a homeostasis mechanism.
October 28, 2025 at 4:01 PM
We introduce constraints to the adaptive dynamics as a way to reduce dimensionality. These may be intrinsic, for example, if the adaptation rule is nondirectional. Or they may be forced by a homeostasis mechanism.
Adaptivity is a crucial ingredient of many networked systems, but a key issue is their high-dimensionality. A dense network of N nodes has O(N^2) adaptive connections.
October 28, 2025 at 4:01 PM
Adaptivity is a crucial ingredient of many networked systems, but a key issue is their high-dimensionality. A dense network of N nodes has O(N^2) adaptive connections.
"Free yourself with constraints" is a good summary of the work.
July 14, 2025 at 11:52 AM
"Free yourself with constraints" is a good summary of the work.
Maybe I should use generative AI to plot any vector field in the style of ancient nails...
June 30, 2025 at 12:38 PM
Maybe I should use generative AI to plot any vector field in the style of ancient nails...
Indeed, great to see so many of you! And of course thanks to @andai.bsky.social and @piratepeel.bsky.social for making NetSci 2025 happen.
June 9, 2025 at 1:43 PM
Indeed, great to see so many of you! And of course thanks to @andai.bsky.social and @piratepeel.bsky.social for making NetSci 2025 happen.

