
In search of statistical intuition for modern ML & simple explanations for complex things👀
Interested in the mysteries of modern ML, causality & all of stats. Opinions my own.
https://aliciacurth.github.io

while there is no difference in kernel weights for GBTs across different input irregularity levels, the neural net’s kernel weights for the most irregular ex grow more extreme! 12/n

while there is no difference in kernel weights for GBTs across different input irregularity levels, the neural net’s kernel weights for the most irregular ex grow more extreme! 12/n
We find that GBTs outperform NNs already in the absence of irregular ex; this speaks to diff in baseline suitability
The performance gap then indeed grows as we increase irregularity!11/n

We find that GBTs outperform NNs already in the absence of irregular ex; this speaks to diff in baseline suitability
The performance gap then indeed grows as we increase irregularity!11/n
Neural net tangent kernels OTOH are generally unbounded and could take on very different vals for unseen test inputs!😰 9/n

Neural net tangent kernels OTOH are generally unbounded and could take on very different vals for unseen test inputs!😰 9/n
A second diff is a lot more subtle and relates to how regular (or: predictable) the two will likely behave on new data: … 8/n

A second diff is a lot more subtle and relates to how regular (or: predictable) the two will likely behave on new data: … 8/n
Surely this diff in kernel must account for at least some of the observed performance differences… 🤔7/n

Surely this diff in kernel must account for at least some of the observed performance differences… 🤔7/n
From our previous work on random forests(arxiv.org/abs/2402.01502) we know we can interpret trees as adaptive kernel smoothers, so we can rewrite the GBT preds as weighted avgs over training loss grads!6/n

From our previous work on random forests(arxiv.org/abs/2402.01502) we know we can interpret trees as adaptive kernel smoothers, so we can rewrite the GBT preds as weighted avgs over training loss grads!6/n
Not to be confused with other forms of boosting (eg Adaboost), *Gradient* boosting fits a sequence of weak learners that execute steepest descent in function space directly by learning to predict the loss gradients of training examples! 5/n

Not to be confused with other forms of boosting (eg Adaboost), *Gradient* boosting fits a sequence of weak learners that execute steepest descent in function space directly by learning to predict the loss gradients of training examples! 5/n
While the severity of the perf gap over neural nets is disputed, arxiv.org/abs/2305.02997 still found as recently as last year that GBTs esp outperform when data is irregular! 3/n

While the severity of the perf gap over neural nets is disputed, arxiv.org/abs/2305.02997 still found as recently as last year that GBTs esp outperform when data is irregular! 3/n
@alanjeffares.bsky.social & I suspected that answers to this are obfuscated by the 2 being considered very different algs🤔
Instead we show they are more similar than you’d think — making their diffs smaller but predictive!🧵1/n

@alanjeffares.bsky.social & I suspected that answers to this are obfuscated by the 2 being considered very different algs🤔
Instead we show they are more similar than you’d think — making their diffs smaller but predictive!🧵1/n
Grokking MNIST experiments use no good inits and no softmax. *With* both, models obv generalise faster — AND need much lower learned complexity! 16/n

Grokking MNIST experiments use no good inits and no softmax. *With* both, models obv generalise faster — AND need much lower learned complexity! 16/n
Using EPs, we reconcile the two & show that onset of performance is associated with divergence of train&test complexity in both! 15/n
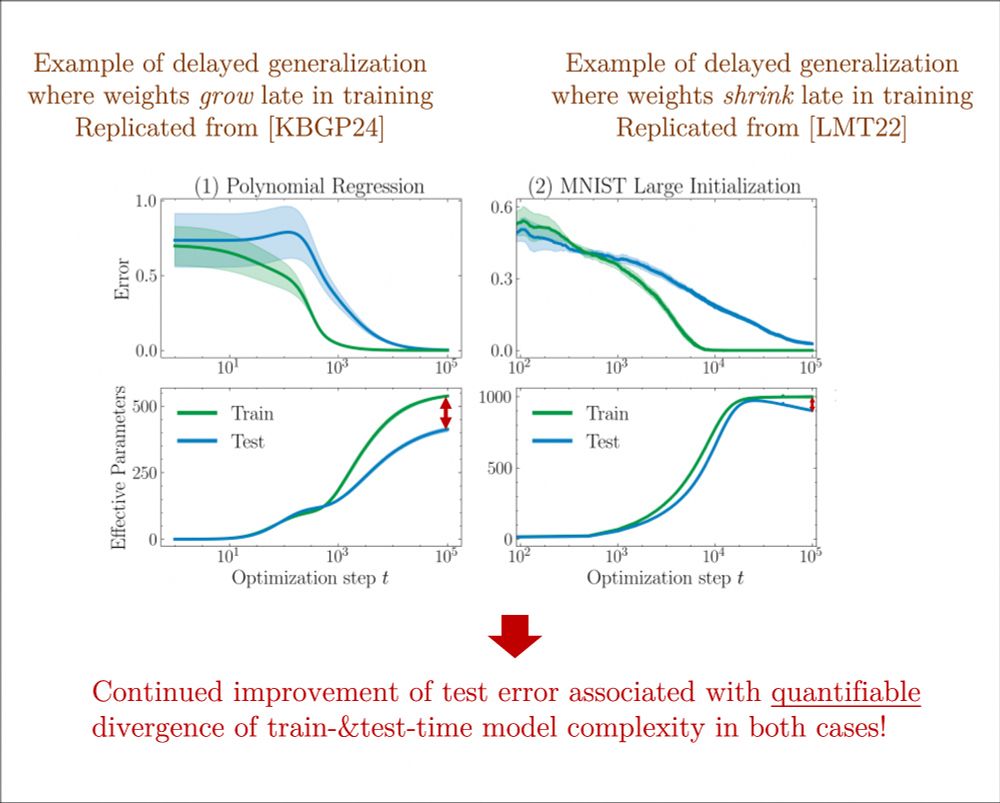
Using EPs, we reconcile the two & show that onset of performance is associated with divergence of train&test complexity in both! 15/n

Now we can compute effective parameters for trained nets! 11/n

Now we can compute effective parameters for trained nets! 11/n
BUT it requires to write predictions as a linear combination of the training labels... 🤔 10/n

BUT it requires to write predictions as a linear combination of the training labels... 🤔 10/n
Intuitively it's not about what models *could* learn, it's all about what they *have learned*! 9/n

Intuitively it's not about what models *could* learn, it's all about what they *have learned*! 9/n
Today I’ll tell you about case study 1: understanding *learned* model complexity! 8/n

Today I’ll tell you about case study 1: understanding *learned* model complexity! 8/n
Essentially by design, it matches the full networks’ predictions more closely -- AND performs categorically more similarly! 7/n

Essentially by design, it matches the full networks’ predictions more closely -- AND performs categorically more similarly! 7/n
For a single step changes are small,so we can better linearly approximate individual steps sequentially(instead of the whole trajectory at once)
➡️ We refer to this as ✨telescoping approx✨!6/n

For a single step changes are small,so we can better linearly approximate individual steps sequentially(instead of the whole trajectory at once)
➡️ We refer to this as ✨telescoping approx✨!6/n
We thus explore a subtly different idea. We ask: “if you give us access to the optimisation trajectory of your trained net, what can we tell you about what it *has* learned in training?” 5/n

We thus explore a subtly different idea. We ask: “if you give us access to the optimisation trajectory of your trained net, what can we tell you about what it *has* learned in training?” 5/n
V neat! BUT… 4/n

V neat! BUT… 4/n
That’s essentially the idea behind the neural tangent kernel/lazy learning literature!! They assume.. 3/n

That’s essentially the idea behind the neural tangent kernel/lazy learning literature!! They assume.. 3/n
Ppl like linear models bc they have none of these problems 2/n

Ppl like linear models bc they have none of these problems 2/n
For NeurIPS(my final PhD paper!), @alanjeffares.bsky.social & I explored if&how smart linearisation can help us better understand&predict numerous odd deep learning phenomena — and learned a lot..🧵1/n
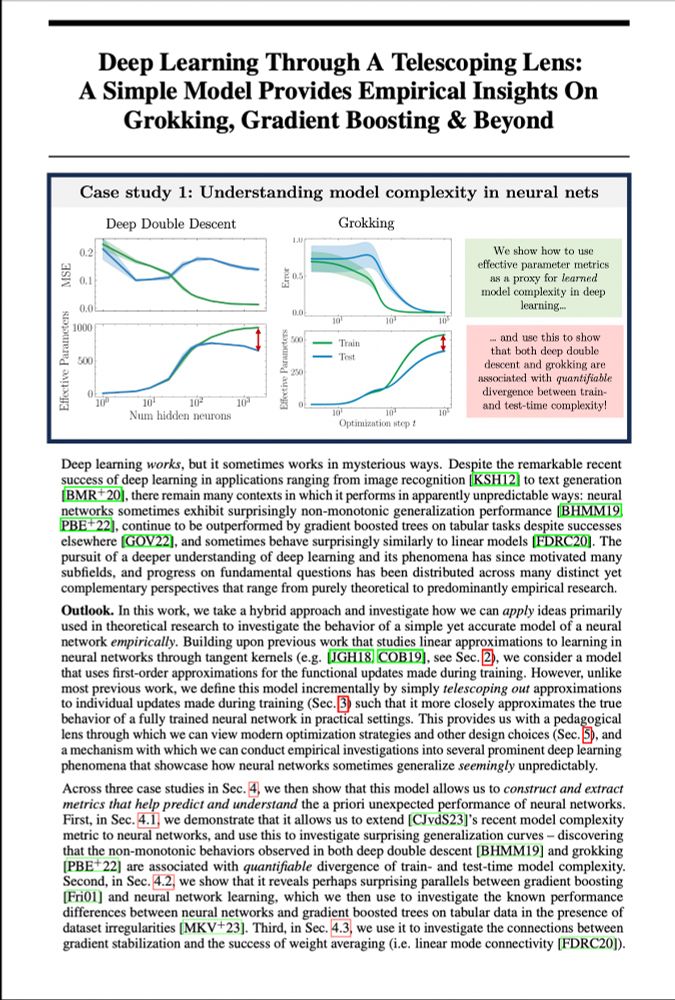
For NeurIPS(my final PhD paper!), @alanjeffares.bsky.social & I explored if&how smart linearisation can help us better understand&predict numerous odd deep learning phenomena — and learned a lot..🧵1/n

